Fair shares: sexual justice in patient recruitment in clinical trials

 

Stephen Senn
Consultant Statistician
Edinburgh, Scotland

It is hard to argue against the proposition that approaches to clinical research should treat not only men but also women fairly, and of course this applies also to other ways one might subdivide patients. However, agreeing to such a principle is not the same as acting on it and when one comes to consider what in practice one might do, it is far from clear what the principle ought to be. In other words, the more one thinks about implementing such a principle the less obvious it becomes as to what it is.

Three possible rules

Suppose we accept that we ought to strive to treat the needs of male and female patients equally. There are three possible approaches we might have.

1. Equality of access and sacrifice. We might suppose that any patient should have the same chance of entering a clinical trial whether they were male or female. This would mean that males and females would have an equal chance of benefitting, if participating in a trial is a benefit, but also have an equal chance of contributing to clinical progress. Note that since men can benefit from the knowledge gained from studying women and vice versa, and since clinical research cannot be guaranteed to be free from risk, it is not always clear whether an overrepresentation of one of the sexes in a clinical trial is an unfair benefit or an unjust exploitation. This particular principle requires that men and women should be represented in clinical trials for a given indication according to the proportion they represent in the patient population.
2. Equality of information. It is a fact not always appreciated by commentators on clinical trials that, other things being equal, the information provided by any group is proportional to the absolute number of patients recruited and not to the proportion they make of the relevant population. Thus, for example, if we design a clinical trial with 100 patients on the intervention arm and 100 patients on the control arm but we wish to make sure that the same amount of information is provided for men as for women, we shall need to have 50 men and 50 women on each of the two arms. Now suppose, however, that for the disease in question the prevalence is greater among women (say) than among men. (Alzheimer’s is an example.) In that case we shall have to over-sample (to use a statistical term) from male patients, if we wish to provide the same amount of information for men as for women. Thus, unless males and females form an equal proportion of patients, the requirement for equality of information will conflict with the requirement for equality of access and sacrifice.
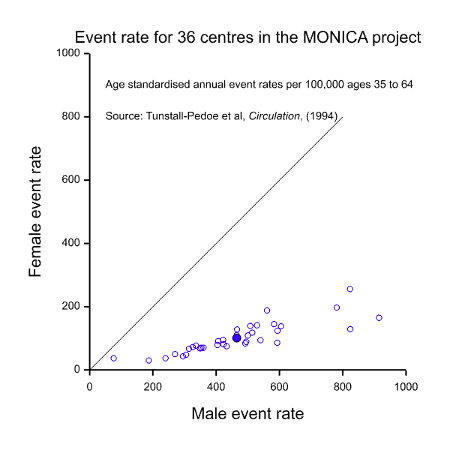
3. Equality of outcome. Now suppose that we have a condition where the prognosis is worse for one of the sexes. Figure 1 gives case fatality rates for coronary heart disease (CHD) in the WHO MONICA project (Tunstall-Pedoe, Kuulasmaa et al. 1994) for patients aged 35 to 64 and plots the value for females against the value for males for 36 participating centres. Most points lie to the left and above the line of equality, as does the point for the mean values (solid blue), indicating that the rate is generally higher and worse for females. This might suggest that more research effort should be devoted to studying women rather than men.

 

Goal conflict

It should be fairly obvious from the above that these three possible interpretations for equality cannot possibly be satisfied in one clinical trial. Take, for example, the situation of CHD illustrated in Figure 1. The MONICA study also obtained data on event rates for CHD. These are illustrated in Figure 2. This shows a dramatic difference between the two sexes but this time it is males who are at a disadvantage. Of course, this dramatic disparity itself calls into question any suggestion that females are at a disadvantage: as with many such things it depends on what and when one conditions. In addition to conditioning on sex, should we condition on having had a CHD (figure 1) or on having reached age 35 without having had a CHD, or on some other event? However, be that as it may, the practical problem is that it indicates that there will be many more cases of CHD in males than in females, so setting out to study as many women as men would involve considerable oversampling of women.

In this case, it might be argued that there is no particular reason why clinical trials in treatments for CHD should not be organised so as to recruit equal numbers of men as women, thus satisfying the equality of information requirement. After all, CHD is not a rare disease. This may, indeed be possible on occasion but often it would make matters more difficult.

The way that randomised clinical trials are usually set up is that centres that are deemed to be capable of delivering enough patients within a given time frame are recruited and then asked to randomise patients into the trial. This is usually a competitive process, so that the numbers of patients per centre will often vary greatly once the trial is completed. It is well known that requiring the numbers to be equal will delay completion of the trial.

There has been a fair amount of theoretical research backed up by empirical findings showing that competitive recruitment can be much faster than that in which centres are required to provide equal numbers (Senn 1998, Anisimov and Fedorov 2007). The disadvantage in terms of time to completion of trials that seek to have equal numbers per centre applies also when there are such requirements for different strata. Trials in CHD in which a total equal target number of male and female patients was set would be likely to finish recruitment to the former before it did so to the latter. Unless the number of centres were increased compared to a conventional trial with no such requirement, which has the effect of increasing operational difficulties and costs, it would take longer to recruit. Thus many trialists might be very reluctant to set such a target.

Irrelevant excuses?

Are these just irrelevant excuses? Nobody supposes that clinical research should be easy. If treating the needs of men and women equally requires that clinical trials should become more difficult is that not just a price that we should pay?

There are several arguments against this line of reasoning.

First, note that we still have not resolved the inherent contradiction between the three possible rules. The discussion in the previous section tended towards the second rule (equality of information) and possibly the third rule (equality of outcome). It was clearly incompatible with the first rule. However, as we showed, even taking the third rule as our guide, it would depend on what we took as our conditioning event. Men appear to have better survival than women having had a CHD event but given that the events are so much more common for them, their overall chance of dying from such an event is higher.

The second point is that it is more or less a necessity that we borrow information in clinical trials. If we didn’t do this, the effect on numbers would be catastrophic. To have the same precision for making independent statements for men and for women as to do so on average would require twice as many subjects. To make plausibly useful statements about the difference between them would require even more (Senn 2021). We are involved with what statisticians call a bias versus variance trade-off. We may imagine that the bias in using averages stays the same whatever the size of the trial given that the proportions of the two sexes recruited onto it is constant. As the size of the trial increases, however, the variance reduces. For small sample sizes, the variance dominates. It is worth accepting the implied bias. Eventually, for a very large trial it becomes worth splitting the results by men and women rather than pooling them. However, very few trials are large enough to make this a useful strategy.

The third point is that resources are constrained. Any request to have a separate precise answer for men and for women alone competes with other projects, such as for example finding better treatments for everybody. Such requests have to be costed.

The fourth point is that clinical trials are not surveys but experiments. They use convenient material to investigate a problem, not material that is typical. A combination of concurrent control, good choice of scale and suitable theory is used to make useful predictions(Senn 2004). Such predictions have to be partly model based. Indeed moving through the various stages of drug development requires borrowing information from various sources to make successful predictions. We use in vitro studies to make predictions about in vivo studies, animals to make predictions about humans, surrogate endpoints to make predictions about therapeutic ones and, on occasion, males to make predictions about females.

Conclusions

I am not arguing against thinking how we could do better for women or, for that matter, men. In her book, Invisible Women, Caroline Criado Perez draws attention to a  higher proportion of adverse reactions amongst female patients compared to male patients (Criado Perez 2019). I have not researched the sources for this claim myself but it seems plausible, since it is a common habit in many indications to give the same dose to women as to men. Women are on average lighter than men, concentration is related directly both to efficacy and side effects and inversely to body size, so that this is something actionable where we could do better. For an interesting application of allometric scaling to pharmacometrics see (Holford 1996).

In the same book, however, she incorrectly claims that the evidence shows that bioequivalence commonly varies by sex. That such differences would be large is implausible. I will not go into the arguments here but her claim is wrong and I refer the interested reader to a previous blog: Invisible Statistics.

In other words, it will depend on context and purpose whether it is appropriate to try and push for more representation of females or perhaps even, on occasion, males in clinical trials. All decisions to do this should be costed because costs, whether in term of patient time, lost opportunities or money are crucial. Criticise if you wish but your criticisms will be more helpful if you calculate. There is nothing quite so conducive to learning as starting with a detailed protocol and trying to improve it whilst also costing your improvements.

Further reading

This topic is treated in two of my books (Senn 2003, Senn 2021). A neglected but brilliant paper that I can recommend is (Piantadosi and Wittes 1993).

References

Anisimov, V. V. and V. V. Fedorov (2007). “Modelling, prediction and adaptive adjustment of recruitment in multicentre trials.” Statistics in Medicine 26(27): 4958-4975.

Criado Perez, C. (2019). Invisible Women: Exposing data bias in a world designed for men. New York, Random House.

Holford, N. H. (1996). “A size standard for pharmacokinetics.” Clin Pharmacokinet 30(5): 329-332.

Piantadosi, S. and J. Wittes (1993). “Politically Correct Clinical-Trials.” Controlled Clinical Trials 14(6): 562-567.

Senn, S. J. (1998). “Some controversies in planning and analysing multi-centre trials.” Statistics in Medicine 17(15-16): 1753-1765; discussion 1799-1800.

Senn, S. J. (2003). Dicing with Death. Cambridge, Cambridge University Press.

Senn, S. J. (2004). “Added Values: Controversies concerning randomization and additivity in clinical trials.” Statistics in Medicine 23(24): 3729-3753.

Senn, S. J. (2021). Statistical issues in drug development. Chichester, John Wiley & Sons.

Tunstall-Pedoe, H., K. Kuulasmaa, P. Amouyel, D. Arveiler, A. M. Rajakangas and A. Pajak (1994). “Myocardial infarction and coronary deaths in the World Health Organization MONICA Project. Registration procedures, event rates, and case-fatality rates in 38 populations from 21 countries in four continents.” Circulation 90(1): 583-612.