.

Stephen Senn
Consultant Statistician
Edinburgh, Scotland

Sepsis sceptic

During an exchange on Twitter, Lawrence Lynn drew my attention to a paper by Laffey and Kavanagh[1]. This makes an interesting, useful and very depressing assessment of the situation as regards clinical trials in critical care. The authors make various claims that RCTs in this field are not useful as currently conducted. I don’t agree with the authors’ logic here although, perhaps, surprisingly, I consider that their conclusion might be true. I propose to discuss this here.

Disclaimer

My ‘knowledge’ of critical care is non-existent. The closest I have come to being involved is membership of various data-safety monitoring boards for sepsis. This is not at all the same as having been involved in planning trials in sepsis let alone critical care more widely.

Your starter for 10

In my opinion, which the reader should check for themselves, the argument of Laffey and Kavanagh has the following steps.

1. The proportion of positive trials in critical care is low. (One out of 20 large trials that concluded recently was positive.)
2. Given that such large trials are preceded by extensive testing, the number of effective treatments being tested in these large trials ought to be at least 50%.
3. “On a statistical basis, it is unlikely that most negative RCTs represent fair conclusions.” (p657).
4. Some may say that this low success rate is due to patients numbers being too few.
5. “But if the intervention is not matched to the patients being studied (eg, the biological target is absent) then the limitation is biological—not statistical—and insistence on greater numbers (or more stringent p-values) will have no effect.” (p657)
6. The entry criteria for most trials rely on consensus definitions, which have high sensitivity, which is what you want for screening but do not have specificity, which is what you need for recruiting for clinical trials.
7. Hence clinical trials include many patients the treatment could not reasonably be expected to help.
8. This may cause a trial to be a ‘false negative’.
9. Trials in which patients are screened based on mechanism will be more promising.
10. Designers of RCTs and clinical trials groups should ensure that proposed RCTs in critical care identify subgroups of patients that match the specific intervention being tested.

Sum mistake

I can agree with a number of these points but some of them are vary debatable. For example no evidence is given for 3.  Instead a confusing argument, based on the ‘one successful trial in 20’ statistic is produced as follows.

For example, if each hypothesis tested had the same a priori probability that was as low as a coin toss, we would expect 50% of RCTs to be positive. The likelihood that 19 out of 20 consecutive such coin tosses would be negative is less than 1 in half a million (1 ÷ 2¹⁹).  (P657)

This is wrong on several counts. First a minor point is that the probability should not be calculated this way. The probability they calculate applies to the case where 19 trials were run, all of which were failures. For 19 out of 20, we have to allow for the fact that there are 20 possible different selections of one trial from 20 and that we perhaps ought to include the more extreme  case of 20 out of 20 anyway. The calculation should thus be (20+1) x ½¹⁹ x ½ = 21/2²⁰ ≈ 10/2¹⁹. This probability is thus about 10 times higher than the one they calculated and therefore about 1 in 50,000. Still, even so,  this is a low probability.

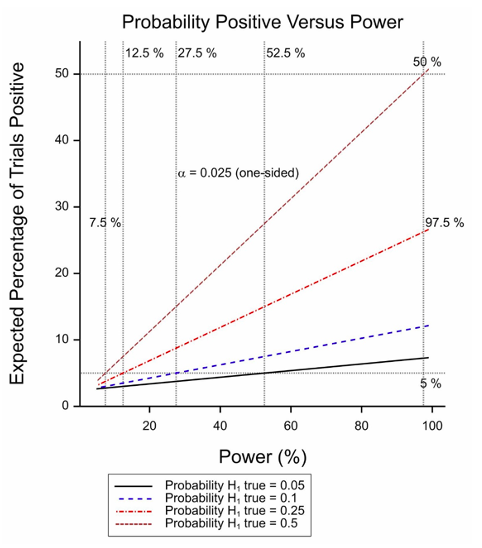
Figure 1 Expected percentage of positive trials as a function of power for various probabilities of the treatment being effective.

The second problem, however, is more serious and is that the calculation takes no account of the power involved. In fact, if half of all null hypotheses are false and the threshold for significance is 2.5% (one sided). Only trials with 97.5% power have a 50% chance of being positive (or an assurance of 50% to use the technical term proposed by O’Hagan, Stevens and Campbell[2]). The situation is illustrated in Figure 1 for various probabilities of the treatment being effective. A combination of a low probability and a moderate power will yield few significant trials.

The third problem, however is that the argument given in 2 and 7 is weak and inconsistent. It supposes that research in early stages of development can succeed in identifying treatments that we can be reasonably confident are effective for some patients but have no idea who they are.

Quite apart from anything else, the problem with this line of arguments is that the ‘responders’ have to be a small proportion of those included for the power to drop to the sort of level that could explain these results.

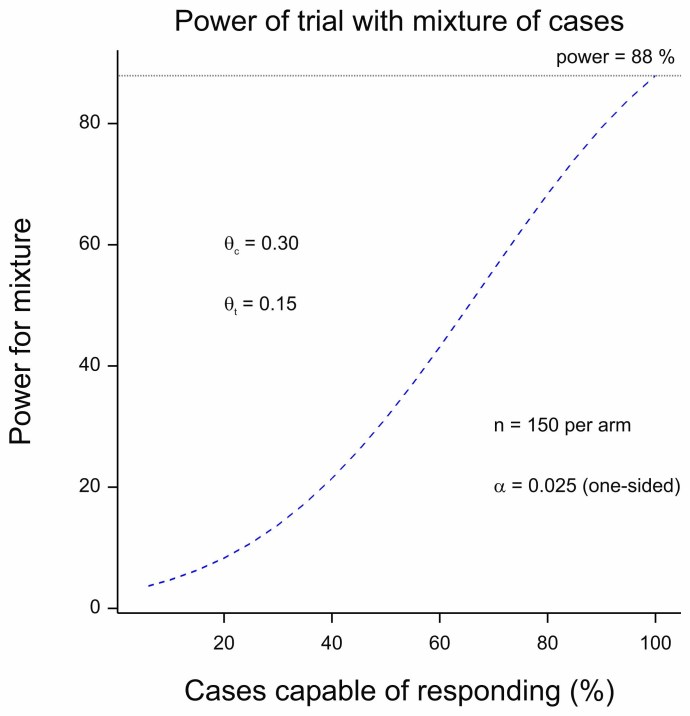
Figure 2 Power for a trial as a function of the proportion of cases capable of responding.

For Figure 2, I used the following. I took some figures from a recent published protocol for “Low-Molecular Weight Heparin dosages in hospitalized patients with severe COVID-19 pneumonia and coagulopathy not requiring invasive mechanical ventilation (COVID-19 HD)”[3]. It is not a particularly close match for the indication discussed here but the COVID theme makes it topical and it serves to make a statistical point. The response is binary (clinical worsening or not) and for power calculations rates of 30% and 15% are compared yielding power in excess of 80% for 150 patients per arm. (I calculate about 88%.) I then supposed that only a percentage of the patients could benefit, the rest having the response probability of the control group. (See chapter 14 of Statistical Issues in Drug Development for a discussion of this approach[4].)

The figure plots the power against the proportion of true responders recruited. When this is 100%, the power reaches 88%. However, even when only one in every two patients is capable of benefitting, the power is 38%. If we now turn to figure 1 we see that if half the treatment works well but in only half the patients (power of 38%), we still expect to see one in five trials being a ‘success’.

Of course, we can always postulate having even larger proportions of non-responders but at what point does it become ludicrous to claim one has a treatment: it works well when it works, only unfortunately there are almost no patients for whom it works?

Naught for your comfort

The sad truth seems to be that the data suggest that effective treatments are not being found in this field. In a sense I agree with the authors’ conclusions. Success will be a matter of finding the right treatments to treat the right patients. I have no quarrel with that. However, my personal hunch is that it will have more to do with finding good drugs than finding the perfect patients. Of course, doing the former may, indeed, require identifying good druggable targets. Nevertheless, when and if the right drugs are found for the right patients, convincing proof will come from a randomised clinical trial. Drug development is easy compared to drug research and I have always worked in the former. Nevertheless, sometimes the unwelcome but true message from development is that research is even harder than supposed.

References

1. Laffey, J.G. and B.P. Kavanagh, Negative trials in critical care: why most research is probably wrong. Lancet Respir Med, 2018. 6(9): p. 659-660.
2. O’Hagan, A., J.W. Stevens, and M.J. Campbell, Assurance in clinical trial design. Pharmaceutical Statistics, 2005. 4(3): p. 187-201.
3. Marietta, M., et al., Randomised controlled trial comparing efficacy and safety of high versus low Low-Molecular Weight Heparin dosages in hospitalized patients with severe COVID-19 pneumonia and coagulopathy not requiring invasive mechanical ventilation (COVID-19 HD): a structured summary of a study protocol. Trials, 2020. 21(1): p. 574.
4. Senn, S.J., Statistical Issues in Drug Development. Statistics in Practice. 2007, Hoboken: Wiley. 498.