Stephen Senn
Head of Competence Center for Methodology and Statistics (CCMS)
Luxembourg Institute of Health
The pathetic P-value
This is the way the story is now often told. RA Fisher is the villain. Scientists were virtuously treading the Bayesian path, when along came Fisher and gave them P-values, which they gladly accepted, because they could get ‘significance’ so much more easily. Nearly a century of corrupt science followed but now there are signs that there is a willingness to return to the path of virtue and having abandoned this horrible Fisherian complication:
We shall not cease from exploration
And the end of all our exploring
Will be to arrive where we started …A condition of complete simplicity..
And all shall be well and
All manner of thing shall be wellTS Eliot, Little Gidding
Consider, for example, distinguished scientist David Colquhoun citing the excellent scientific journalist Robert Matthews as follows
“There is an element of truth in the conclusion of a perspicacious journalist:
‘The plain fact is that 70 years ago Ronald Fisher gave scientists a mathematical machine for turning baloney into breakthroughs, and flukes into funding. It is time to pull the plug. ‘
Robert Matthews Sunday Telegraph, 13 September 1998.” [1]
However, this is not a plain fact but just plain wrong. Even if P-values were the guilty ‘mathematical machine’ they are portrayed to be, it is not RA Fisher’s fault. Putting the historical record right helps one to understand the issues better. As I shall argue, at the heart of this is not a disagreement between Bayesian and frequentist approaches but between two Bayesian approaches: it is a conflict to do with the choice of prior distributions[2].
Fisher did not persuade scientists to calculate P-values rather than Bayesian posterior probabilities; he persuaded them that the probabilities that they were already calculating and interpreting as posterior probabilities relied for this interpretation on a doubtful assumption. He proposed to replace this interpretation with one that did not rely on the assumption.
To understand this, consider Student’s key paper[3] of 1908, in which the following statement may be found:
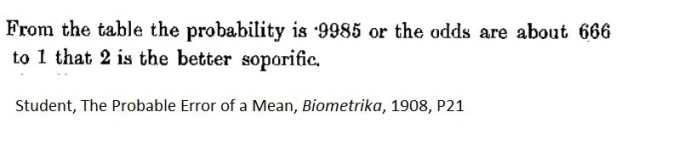 Student was comparing two treatments that Cushny and Peebles had considered in their trials of optical isomers at the Insane Asylum at Kalamazoo[4]. The t-statistic for the difference between the two means (in its modern form as proposed by Fisher) would be 4.06 on 9 degrees of freedom. The cumulative probability of this is 0.99858 or 0.9986 to 4 decimal places. However, given the constraints under which Student had to labour, 0.9985 is remarkably accurate and he calculated 0.9985/(1-0.9985)= 666 to 3 decimal places and interpreted this in terms of what a modern Bayesian would call posterior odds. Note that right-hand probability corresponding to Student’s left hand 0.9885 is 0.0015 and is, in modern parlance, the one-tailed P-value.
Student was comparing two treatments that Cushny and Peebles had considered in their trials of optical isomers at the Insane Asylum at Kalamazoo[4]. The t-statistic for the difference between the two means (in its modern form as proposed by Fisher) would be 4.06 on 9 degrees of freedom. The cumulative probability of this is 0.99858 or 0.9986 to 4 decimal places. However, given the constraints under which Student had to labour, 0.9985 is remarkably accurate and he calculated 0.9985/(1-0.9985)= 666 to 3 decimal places and interpreted this in terms of what a modern Bayesian would call posterior odds. Note that right-hand probability corresponding to Student’s left hand 0.9885 is 0.0015 and is, in modern parlance, the one-tailed P-value.
Where did Student get this method of calculation from? His own innovation was in deriving the appropriate distribution for what later came to be known as the t-statistic but the general method of calculating an inverse probability from the distribution of the statistic was much older and associated with Laplace. In his influential monograph, Statistical Methods for Research Workers[5], Fisher, however, proposed an alternative more modest interpretation, stating:
(Here n is the degrees of freedom and not the sample size.) In fact, Fisher does not even give a P-value here but merely notes that the probability is less than some agreed ‘significance’ threshold.
Comparing Fisher here to Student, and even making allowance for the fact that Student has calculated the ‘exact probability’ whereas Fisher, as a consequence of the way he had constructed his own table (entering at fixed pre-determined probability levels), merely gives a threshold, it is hard to claim that Fisher is somehow responsible for a more exaggerated interpretation of the probability concerned. In fact, Fisher has compared the observed value of 4.06 to a two-tailed critical value, a point that is controversial but cannot be represented as being more liberal than Student’s approach.
To understand where the objection of some modern Bayesians to P-values comes from, we have to look to work that came after Fisher, not before him. The chief actor in the drama was Harold Jeffreys whose Theory of Probability[6] first appeared in 1939, by which time Statistical Methods for Research Workers was already in its seventh edition.
Jeffreys had been much impressed by work of the Cambridge philosopher CD Broad who had pointed out that the principle of insufficient reason might lead one to suppose that, given a large series of only positive trials, the next would also be positive but could not lead one to conclude that all future trials would be. In fact, if the future series was large compared to the preceding observations, the probability was small[7, 8]. Jeffreys wished to show that induction could provide a basis for establishing the (probable) truth of scientific laws. This required lumps of probability on simpler forms of the law, rather than the smooth distribution associated with Laplace. Given a comparison of two treatments (as in Student’s case) the simpler form of the law might require only one parameter for their two means, or equivalently, that the parameter for their difference, τ , was zero. To translate this into the Neyman-Pearson framework requires testing something like
H0: τ = 0 v H1: τ ≠ 0 (1)
It seems, however, that Student was considering something like
H0: τ ≤ 0 v H1: τ > 0, (2)
although he perhaps also ought simultaneously to be considering something like
H0: τ ≥0 v H1: τ < 0, (3)
although, again, in a Bayesian framework this is perhaps unnecessary.
(See David Cox[9] for a discussion of the difference between plausible and dividing hypotheses.)
Now the interesting thing about all this is if you choose between (1) on the one hand and (2) or (3) on the other, it makes remarkably little difference to the inference you make in a frequentist framework. You can see this as either a strength or a weakness and is largely to do with the fact that the P-value is calculated under the null hypothesis and that in (2) and (3) the most extreme value, which is used for the calculation, is the same as that in (1). However if you try and express the situations covered by (1) on the one hand and (2) and (3) on the other, it terms of prior distributions and proceed to a Bayesian analysis, then it can make a radical difference, basically because all the other values in H0 in (2) and (3) have even less support than the value of H0 in (1). This is the origin of the problem: there is a strong difference in results according to the Bayesian formulation. It is rather disingenuous to represent it as a problem with P-values per se.
To do so, you would have to claim, at least, that the Laplace, Student etc Bayesian formulation is always less appropriate than the Jeffreys one. In Twitter exchanges with me, David Colquhoun has vigorously defended the position that (1) is what scientists do, even going so far as to state that all life-scientists do this. I disagree. My reading of the literature is that jobbing scientists don’t know what they do. The typical paper says something about the statistical methods, may mention the significance level but does not define the hypothesis being tested. In fact, a paper in the same journal and same year as Colquhoun’s affords an example. Smyth et al[10], have 17 lines on statistical methods, including permutation tests (of which Colquhoun approves) but nothing about hypotheses, plausible, point, precise, dividing or otherwise, although the paper does, subsequently, contain a number of P-values.
In other words scientists don’t bother to state which of (1) on the one hand or (2) and (3) on the other is relevant. It might be that they should but it is not clear if they did, which way they would jump. Certainly, in drug development I could argue that the most important thing is to avoid deciding that the new treatment is better than the standard, when in fact it is worse and this is certainly an important concern in developing treatments for rare diseases, a topic on which I research. True Bayesian scientists, of course, would have to admit that many intermediate positions are possible. Ultimately, however, if we are concerned about the real false discovery rate, rather than what scientists should coherently believe about it, it is the actual distribution of effects that matters rather than their distribution in my head, or, for that matter, David Colquhoun’s. Here a dram of data is worth a pint of pontification and some interesting evidence as regards clinical trials is given by Djulbegovic et al[11].
Furthermore, in the one area, model-fitting, where the business of comparing simpler versus complex laws is important, rather than, say, deciding which of two treatments is better (note that in the latter case a wrong decision has more serious consequences), then a common finding is not that the significance test using the 5% level is liberal but that it is conservative. The AIC criterion will choose a complex law more easily and although there is no such general rule about the BIC, because of its dependence on sample size, when one surveys this area it is hard to come to the conclusion that significance tests are generally more liberal.
Finally, I want to make it clear, that I am not suggesting that P-values alone are a good way to summarise results, nor am I suggesting that Bayesian analysis is necessarily bad. I am suggesting, however, that Bayes is hard and pointing the finger at P-values ducks the issue. Bayesians (quite rightly so according to the theory) have every right to disagree with each other. This is the origin of the problem and to therefore dismiss P-values
‘…would require that a procedure is dismissed because, when combined with information which it doesn’t require and which may not exist, it disagrees with a procedure that disagrees with itself.’[2] (p 195)
Acknowledgement
My research on inference for small populations is carried out in the framework of the IDEAL project http://www.ideal.rwth-aachen.de/ and supported by the European Union’s Seventh Framework Programme for research, technological development and demonstration under Grant Agreement no 602552.
References
- Colquhoun, D., An investigation of the false discovery rate and the misinterpretation of p-values. Royal Society Open Science, 2014. 1(3): p. 140216.
- Senn, S.J., Two cheers for P-values. Journal of Epidemiology and Biostatistics, 2001. 6(2): p. 193-204.
- Student, The probable error of a mean. Biometrika, 1908. 6: p. 1-25.
- Senn, S.J. and W. Richardson, The first t-test. Statistics in Medicine, 1994. 13(8): p. 785-803.
- Fisher, R.A., Statistical Methods for Research Workers, in Statistical Methods, Experimental Design and Scientific Inference, J.H. Bennet, Editor 1990, Oxford University: Oxford.
- Jeffreys, H., Theory of Probability. Third ed1961, Oxford: Clarendon Press.
- Senn, S.J., Dicing with Death2003, Cambridge: Cambridge University Press.
- Senn, S.J., Comment on “Harold Jeffreys’s Theory of Probability Revisited”. Statistical Science, 2009. 24(2): p. 185-186.
- Cox, D.R., The role of significance tests. Scandinavian Journal of Statistics, 1977. 4: p. 49-70.
- Smyth, A.K., et al., The use of body condition and haematology to detect widespread threatening processes in sleepy lizards (Tiliqua rugosa) in two agricultural environments. Royal Society Open Science, 2014. 1(4): p. 140257.
- Djulbegovic, B., et al., Medical research: trial unpredictability yields predictable therapy gains. Nature, 2013. 500(7463): p. 395-396.







I think this glosses one of the two major reasons that Bayesians dislike p values. You talk about the first, but the more fundamental one is simply that there’s no justification for the epistemic conclusions (“feelings of reluctance”) that Fisher suggested could be drawn from the p value. A Bayesian must interpret the conclusion in light of the prior, so the epistemic claims are circumscribed. But scientists, in using a p value to reject (not in Neyman’s behavioural sense, but in Fisher’s epistemic sense, as implausible) are circumventing their responsibility to have a *reason* for belief. To borrow a phrase, p values attempt to make an epistemic omelet with out breaking any epistemic eggs.
Subjective Bayesians would thus agree with Neyman’s (1957) critique of both Fisher: “[I]f a scientist inquires why should he reject or accept hypotheses in accordance with the calculated values of p the unequivocal answer is: because these values of p are the ultimate measures of beliefs especially designed for the scientist to adjust his attitudes to. If one inquires why should one use the normative formulae of one school rather than those of some other, one becomes involved in a fruitless argument.” (Neyman also correctly argued against Jeffreys along the same lines).
This is, in my opinion, the most fundamental critique of p values, and as Neyman hinted, it aligns frequentists and subjectivists on the same side (but with different resolutions).
Richard: Neyman’s disavowal of any universal measure for rational inductive inference was indeed right-headed, but the differences between Fisher and Neyman aren’t really very large. When Fisher is talking about this degree of reluctance he is actually explaining why a prior probability (e.g., to the stars being arrayed at random)–never minding how you got it–would not remove the strong evidence against the null even if it resulted in a high posterior in the null (of random distribution). Anyway, I take Senn to be focusing on a specific issue which goes back to my discussion of the charge that p-values allegedly exaggerate evidence. I’ll give a couple of links below:
First, I’d like to thank Stephen Senn for many discussions about the problems discussed here. I’ve learnt a lot from them. I still can’t claim to understand fully all the problems, but neither, it seems do professional statisticians. It remains true, as I said in 1971,
I think that there are at least three relevant issues
1) Whether noting the probability of a result as extreme or more extreme is of any interest
2) Whether calculating P-values causes scientists to conclude significance more easily than if they were to use Bayesian approaches
3) Whether banning P-values will resolve the conflict
The point of my post is the following. Even if you think that 1) is of no interest and even if you proceed to implement 3) you will have your work cut out if you want to make scientists more conservative because 2) is not the source of the “problem”.
So I can agree with you, that Bayesians may object to P-values because they dislike the interpretation. However, much of the recent attack on P-values is precisely because significance tests are deemed to be too liberal. The first of my 11 references was to David Colquhoun’s paper, which claims exactly that and which was the inspiration for this piece..
In fact, any survey of Bayesian practice will show that Laplace rules compared to Jeffreys. Furthermore, those who do promote Jeffreys’s approach to significance testing but want to retain the 1/20 standard for significance have misunderstood the implication of the simplicity postulate. This (if the editor of Error Statistics Philosophy permits) will be the subject of a second post.
First, I’d like to thank Stephen Senn for many discussions about the problems discussed here. I’ve learnt a lot from them. I still can’t claim to understand fully all the problems, but neither, it seems do professional statisticians. It remains true, as I said in 1971,
“It is difficult to give a consensus of informed opinion because, although there is much informed opinion, there is rather little consensus. A personal view follows”.
Of course the quotation from Matthews is much too harsh on Fisher. I interpret the quotation to refer to the whole business of null hypothesis significance testing, as universally practised by most experimenters.
I think that it is indubitably true that what experimenters need to know is the false discovery rate (FDR), so I’m a bit surprised that it isn’t mentioned in this post. Very frequently experimenters make the mistake of equating that with the P value. The problem lies in the fact that there is no unique way of calculating the FDR and no unique relationship between the FDR and the P value. Nevertheless the work of Berger & Sellke, and the work of Valen Johnson on uniformly most powerful Bayesian tests, seems to me to allow one to make a good guess at the minimum FDR. The fact that the minimum FDR can be alarmingly high seems to me to be potentially an important contribution to the crisis of irreproducibility.
I take the point about the different ways that the null hypothesis can be defined, but those objections seem to apply to one-sided tests, whereas in real life two-sided tests are ubiquitous. The only time you see a one-sided test is when somebody gets P = 0.06 (2-sided) and wants to be able to claim a discovery.
The common practice is to use a point null -the difference is exactly zero. Admittedly this is often not stated or even realised by the experimenter, but it’s standard. This seems to me to be entirely appropriate thing to do. We wish to rule out the possibility that the treatment and control are the same (as would be exactly the case if both groups were given the same pill, or if both groups were give homeopathic pills with different labels but identical constitution). If a difference is detected then the question of whether the effect is gig enough to matter is then judged from the estimate of effect size.
In my paper, I provide simulations of repeated t tests (with an R script so you can do them yourself). This mimics precisely what almost everyone does in real life (though, unlike in real life, the ‘experiments’ are perfectly randomised and obey all assumptions exactly). If you use P = 0.05, the simulations show a false discovery rate of at least 26% even for a 50-50 prior, and much higher for lower priors. This should surely be a matter of concern to experimenters. And to statisticians too.
David: Even if you played the game of assigning priors to a hypotheses by randomly picking them from urns of priors assumed to have a known % of true hypotheses, how would you know which urn was relevant for my hypothesis H. Placing the same hypothesis in a different urn, yields a different “prior”. The reference class problem looms large. Moreover, I deny you’d ever know the % of “true” and “false” hypotheses in the urn; you might know a % that haven’t been rejected yet because of insevere probes of their errors yielding innocence by association. Or, if you draw from an urn of associations in a field with a huge “crud factor” like psychology and the social sciences–and these would be genuine associations (as Meehl showed)– you will get a high value of your beloved (yet irrelevant for inference) PPV number.
See my comment on J. Berger (2003), pp. 19-24:
Click to access Berger%20Could%20Fisher%20Jeffreys%20and%20Neyman%20have%20agreed%20on%20testing%20with%20Commentary.pdf
Stephen: I thank you for providing this guest post.
There are a number of other posts of yours that relate to this that I’ll link to later on.
Can you remind me of that paper of yours with the quote that is somewhat analogous to Jeffreys’? You know which I mean.I’d like to link to it.
I’m at that point of my book-writing that I’m keeping a lot under wraps, so not posting too much, though tempted.
The paper is Two Cheers for P-Values. http://www.stat.washington.edu/peter/342/Senn.pdf p195
(I also have an unpublished paper giving a paradox of Bayesian significance tests that says something similar.)
I’ll confess that I’m totally baffled by your description of the false discovery rate as being “irrelevant for inference”. It seems to me to be what matters (and what only too many experimenters think they’ve got when they use a fixed P value).
David: Not only is there the far-fetchedness and subjectivity of deciding which urn my new hypothesis should be regarded as having been randomly selected from (none in fact), but there is the fact that the prevalence in that urn (a notion relevant only for diagnostic screening, but I’m playing along) is irrelevant for whether my hypothesis was well tested, reproducible or the like. I just gave an example: randomly select from a field with a large crud factor, and voila! large PPV, even for lousily warranted hypotheses. Now my hypothesis came from a field with a lot of unsolved problems–it’s on prion diseases and mad caw, say. But instead of going to press the first time I got a significant result I obeyed Fisher who insisted we are uninterested in isolated significant results (unlike what Ioannidis apparently has been taught), and that one has evidence of a genuine experimental effect only when one knows how to generate the statistically significant effect fairly often. I’ve given this quote often enough. I deliberately subjected my hypothesis to a severe error probe as Fisher required before going to press. Then even if my hypotheses came from a field with very rare success rate, there’s good evidence my published effect is genuine, or that if incorrect, it’s flaws will ramify in further checks. In fact, the boldness of my hypotheses, together with the error probing, results in a far more severely tested (not to mention more interesting) hypothesis than the one with high PPV from the high crud factor field. A high PPV’s got nothing to do with replicability or genuineness of effect, in and of itself. What’s doing the work, or failing to do the work, is lack of distorting selecting effects, lack of bias, following Fisher’s requirements.
David and I have had some vigorous exchanges on this over the past few days in which the FDR has appeared. I quote what i said to him in one of these
”
one must distinguish between
1) The true FDR
2) The FDR that applies to a given subjective prior entertained by a scientist (or group of scientists)
You can defend 2) as being more important than 1) but this just means that you really are a subjective Bayesian uninterested in frequencies. If you are interested in frequencies, then you can’t use your claim that scientists think…”
a given way…
“(which I dispute anyway) as a defence of your simulation. After all, you maintain that scientist are wrong to like P-values so maybe they are wrong in what they think about hypotheses. I gave you empirical evidence(1) regarding the distribution of effects but you have ignored it.
I can sum it up like this: drugs pay no attention in what they do to what scientists think. In what they think scientists should pay some attention to what drugs do.”
Furthermore citing the fact that two-sided tests are used as an argument that scientists use plausible null hypotheses rather than dividing null hypotheses is wrong. A whole chapter of my book Statistical Issues in Drug Development http://www.senns.demon.co.uk/SIDD.html is devoted to this and I have already provided David with a copy.
Reference
(1) Djulbegovic, B., et al., Medical research: trial unpredictability yields predictable therapy gains. Nature, 2013. 500(7463): p. 395-396.
Stephen: I’m not familiar with the particular discourse you’ve had with David C, but, as I understand it, rejecting a “dividing” null just means there’s evidence of the direction of the effect, whereas failing to reject indicates the test wasn’t even sensitive enough to point to the direction. (This is from D. Cox). What I’m not immediately seeing is the connection to the PPV/FDR business.
To general readers: I apologize in not having time to spell out the defns and background from diagnostic screening, in the middle of travels.
Stephen
I have read your chapter 12 (for which, thanks very much). It raises no objections to the convention of using two-sided tests, and it doesn’t seem to discuss the matters that we are talking about here.
Section 12.2.2, 12.2.3, & 12.2.4 all give arguments as to why two sided tests do not need to be associated with plausible hypotheses. If you read my blog post you will see that Student did not consider a plausible hyyothesis but a dividing one (but then Jeffreys’s work lay 31 years in the future) and despite that, Fisher proposed a two-sided P-value.
In any case, as I have already pointed out double guessing what’s inside scientists’ head is not directly relevant to determining true false discover rates.
@Mayo
Can you please explain the sense in which my simulated t tests are dependent on “assigning priors to a hypotheses by randomly picking them from urns of priors”?
They are simply mimicking what’s done in real life. The prior is irrelevant in the sense that the most optimist prior still gives a 26% false discovery rate. It could, of course, be much higher than that, but that’s the minimum.
The logic of the parent post seems strange.
1) Statisticians wanted posterior probabilities; but Fisher highlighted that what they were calculating (P-values) were not posterior probabilities, and instead explained what they were. So p-values are okay.
=> It seems to me the moral of this is not to do the same old calculations and call them p-values; but instead, if what you want are posterior probabilities, do better calculations (eg FDR) that with luck *do* give a more reasonable estimate for the posterior probability.
2) P-values aren’t always wrong by being too liberal (ie an underestimate for the false discovery rate) — in other cases they are wrong by being too conservative (ie an overestimate for the false discovery rate). So p-values are okay.
=> I’m not sure why showing that p-values can be differently misleading is supposed to be comforting. Again, if one is interested in trying to evaluate the false discovery rate (which one probably is), the clearer moral would seem to be: don’t make the mistake of thinking a p-value necessarily gives a good estimate of the FDR.
It was interesting recently, doing an MSc in bioinformatics, the FDR was very much presented as the current metric of choice, on the basis that with large datasets and very large numbers of hypotheses it very often *can* be estimated empirically pretty well; (or as DC indicates, there is also the option to calculate theoretical bounds) — whereas such settings generally expose the inadequacies of p-values.
(I must also say, while I’m here, that I did very much enjoy “Dicing with Death”, which I picked up as light relief at the same time — thank you!)
JH I think that this is not an entirely reasonable representation of my parent post, which was not really about whether P-values are in themselves reasonable or not.This was an issue I felt it was not necessary to explore. I pointed out that the history had been somewhat distorted and this distortion hides a problem that will not go away by banning P-values.
Take a concrete example where (similar to the case Student considered) comparing drug B to drug A with B apparently having a better effect, Fisher would calculate a P-value (two sided ) of 0.04, (say). What would Student the Bayesian (to use an anachronism) calculate? He would calculate that the probability that B was really better than A was 0.98. If banning P-values leads people to do this, then it is hard to see how David Colqhoun’s criticism would be answered.
However, it would have the advantage of having the real origin of the difference exposed: very little to do with choice of framework, a great deal to do with choice of prior distribution.
DC thinks we should be calculating FDRs but if so I would rather be hanged for a sheep than a lamb. I would rather do some serious thinking about what is a reasonable prior distribution than use either Student-Laplace or Jeffreys -but once you sip the Bayesian poison (or ambrosia) then you have to drain the cup to the dregs.
This is not just talk. I have actually proposed that something serious could be done for random effect meta-analysis. See (1)
However, what I do think is completely pointless is producing a chimeric re-calibrated P-values that is neither fish nor fowl nor good red herring.
However, as regards empirical FDR calculation for large datasets – go ahead! Nicola Greenlaw, did an MSc with me in which she examined empirically the possibility that random effect variances are correlated with treatment effects by looking at 125 meta-analyses. (As I predicted, they are.)
Thanks for the puff for Dicing with Death! 🙂
Reference
(1) Senn, S. J. (2007). “Trying to be precise about vagueness.” Statistics in Medicine 26: 1417-1430.
A previous investigation by Lambert et al., which used computer simulation to examine the influence of choice of prior distribution on inferences from Bayesian random effects meta-analysis, is critically examined from a number of viewpoints. The practical example used is shown to be problematic. The various prior distributions are shown to be unreasonable in terms of what they imply about the joint distribution of the overall treatment effect and the random effects variance. An alternative form of prior distribution is tentatively proposed. Finally, some practical recommendations are made that stress the value both of fixed effect analyses and of frequentist approaches as well as various diagnostic investigations.
> When Fisher is talking about this degree of reluctance he is actually explaining why a prior probability (e.g., to the stars being arrayed at random)–never minding how you got it–would not remove the strong evidence against the null even if it resulted in a high posterior in the null
Fisher had no formal account of the relationship between evidence and belief, nor of how “strong evidence” could/could not be “removed” by some prior probability (could “weak evidence” be “removed”? How?), so the same critique still applies.
> However, much of the recent attack on P-values is precisely because significance tests are deemed to be too liberal.
Before this question becomes meaningful, one must have a formalization of evidence, and the strength thereof, in mind. Fisher never offered one that wasn’t begging the question. Any Bayesian arguing to a non-Bayesian about whether p values are too liberal is conceding too much and confusing the issue.
Just in case anybody misunderstands, I’m certainly not proposing to ban P values. They do what they say and are clearly useful. In practice the problem of FDR can be dealt with largely simply by changing the words that are used to describe P values. I have made some suggestions at http://rsos.royalsocietypublishing.org/content/1/3/140216#comment-1889100957
In contrast, the words “significant” and “not significant” certainly should be banned.
David: It seems that one can only know the FDR after the experiment is done and if through some independent means the truth is ascertained (comparison to a gold standard?). When you do a simulation, you control the FDR within some bounds by first setting the proportion of true nulls. If you change your simulation to have, for example, all true nulls and re-run it, do you not get an FDR close to 1? If you have no true nulls is it not close to 0? My understanding of Mayo’s point is that if you want to simulate some kind of scientific practice more generally, then you have to model how often the null hypotheses are true in the real world. Who thinks they are true 50% of the time?
In real research, you cannot know the actual FDR if you cannot know what proportion of the null hypotheses are true. If you are often dealing with true nulls,then FDR may be high and that is just the way it has to be. That is expected. You cannot predict what all of us should get in using t-tests, for example, because it will depend on a lot more than the statistical test chosen. This seems to me to be a broader issue than the merits of p-values.
I believe it is for these reasons that Benjamini and Hochberg provide a method for controlling the family-wise error rate that is based upon the expected FDR.
John: With tests nearly free of “bias” as Ioannidis defines it, the PPVs are quite high for small alpha, high power–basically the alpha error rate holds good–he has to introduce bias to get bad PPVs. But I still say they are irrelevant to truth, warrant, replicability.
I find it amazing, by the way, that people could castigate Neyman for daring to care about error rates in the long run (even though he largely used them to measure the capabilities of tests in the short run) while embracing this new-fangled science-wise error rates over different hypotheses for purposes of appraising a given scientific hypothesis H. There’s a place for empirical Bayes, but even it differs from high throughput diagnostics which says nothing about the well-testedness of the individual hypothesis.
Now if the urn contains hypotheses tested to a given degree of severity, then the fact that your hypothesis is one of those IS relevant, but you didn’t need the make-believe urn, you already get this from the error probabilities of tests.
The whole recommendation of Ioannidis that we keep to safe hypotheses, that we work with hypotheses already known to be true, is a recipe for boring science that never makes bold leaps. And of course there’s the trade-off meaning that we would miss novel claims.
What I find pathetic is to recommend “safe science” rather than mandate responsible science done with integrity, and serious self-criticism. It’s like, keep your bad behavior of going to press based on a single low p-value, and retain your naughty significance seeking and cherry picking, just start with what you think is a barrel with high enough prevalence of truth to keep the overall truth rate decent.
I recognize that this may be distant from what David and Stephen were talking about in an earlier exchange which I’m not aware of.
@john byrd
As I have said repeatedly, you can’t know the FDR without knowing what proportion of null hypotheses are false (what I call P(real) in my paper). But you can show that the minimum FDR is 26% if you use P=0.05 in simulated t tests It will be much higher than that is P(real) is less than 0.5. This is quite sufficient to show that P values are seriously misleading in the common case of testing the difference between two means with a t test.
David: No, although i hate to even take this view of “seriously misleading” seriously. Ioannidis shows that the PPV associated with a .05 sig difference exceeds .5 if (1-beta)R > .05. So wiith R = odds ratio of 1 (.5 priors), you merely need the power to exceed .05! Without bias the PPV would be .95!
There’s a lot wrong with using power this way, and reducing to two hypothesis: the null and the alternative against which the test has high power (as I’ve discussed before) but if we take this game seriously, we still get good numbers. Reading off Ioannidis chart, even with some bias (.1) and power of .8, we get .85 for the PPV (again with odds ratio R = 1).
Mayo
If you can point out the error in my simulations, I’d be eternally grateful.
David: These are analytical computations from screening equations as given in Ioannidis 2005. Without bias, the PPV = .95 where R, prior prevalence odds, is 1 as you say–exactly the .05 error rate promised by tests. I still hold the PPV is an irrelevant computation for statistical inference unless one is in the business of declaring a specific hypothesis H’ well tested so long as H’ was generated by some procedure or other which on average in the long run often spews out true claims, never mind how well-tested H’ is in the reference class of the test at hand. We are back to Cox 1958.
Why should social sciences with huge “crud factors” (these are genuine associations) get the benefit of a high PPV?
I also think that counting up total numbers of effects is open to flim flam: we have continuous parameters, so there may be uncountably many hypotheses.
And even for a given counting procedure, how do we know the % “true” in a given barrel of nulls (from which my null was allegedly randomly selected)? We’d need to use another method to test the truth of the nulls in the barrel, and what would the error rates of that method be?
When Ioannidis tried to get his numbers to show up, “false” had to slide away from the pure dichotomy we were supposed to be limited to. I’m not sure he ever did get them.
I could go on but this is Senn’s post, and I’m getting on a bus.
Mayo
The reason for the discrepancy is that Ioannidis’ 2×2 table is the same thing as my tree diagrams (the latter are a much clearer way of expressing the same idea, in my opinion). From the tree diagrams I get a false discovery rate of 6% (not 5%) for P =< 0.05 and p(H) = 0,5, so there is no serious disagreement between us.
But the problem that I posed was how should you interpret a single test the gives P = 0.047. There seems to be wide agreement that in order to do this. one should look only at tests that come out with P close to 0.047. In the simulations I look at tests that give 0.045 < P < 0.05. This is what gives a false discovery rate (false positive rate) of 26% for P(H) = 0.5 and a lot worse than 26% for smaller P(H). For example, if P(H) = 0.1 the false discovery rate is 76% (see section 10 in http://rsos.royalsocietypublishing.org/content/1/3/140216 ).
If that does not mean there is a problem with P values, I don't know what does.
The spike .5 prior on the null is not innocent or impartial.
Casella and R. Berger (1987) show that “concentrating mass on the point null hypothesis is biasing the prior in favor of H0 as much as possible” (p. 111) whether in 1 or 2-sided tests.
You might want to look at the following post:
Note, too, the conflict with confidence interval reasoning since the null value (here it is 0) lies outside the corresponding confidence interval (Mayo 2005). See Senn’s very interesting points on this same issue in his letter (to Goodman) here.
David (and Stephen, and Mayo), do p(H), p(real) or the FDR even have well-defined frequentist interpretations? What is the process that leads to this probability? The proportion of possible hypotheses that all scientists might have about experiments actually done? The proportion of possible experiments that could be done by existing scientists? The proportion of possible experiments that could be done by all possible scientists?
It seems like p(real) and the FDR have no non-Bayesian meaning at all (and for that matter, barely any Bayesian meaning, for a similar reason).
I maintain that in particular cases they do have a frequentist meaning. If you consider a series of 1000 trial drugs, some will be active, some won’t (and you’d be very lucky indeed if half of them were active. In principal, with sufficient work, it would be possible to determine the proportion. It’s a perfectly normal frequentist probability.
It’s true that you are unlikely to know its value, but that doesn’t matter much. It’s quite enough to know that if you observe P = 0.047 and claim you have made a discovery, you’ll be wrong in at least 26% of cases.
David: A measure can have frequentist meaning without it measuring something relevant to what you think you’re measuring. I’m not denying their usual role in screening, where dichotomy rules. Even there the reference class problem is severe, and your chances of whatever disease, say, differ enormously. Almost no one knows what group to put themselves in even with diseases.
In any event dichotomy accept/reject should not rule in scientific inference–isn’t that we all want tests to move AWAY from? In fact the two hypotheses do not exhaust the space.
Your last assertion is self contradictory–you know the value while you don’t know the value. We don’t even know what the world of “cases” are, but we interested in how good a job you did in this case, and high PPV doesn’t mean you have, and low PPV doesn’t mean you haven’t. It’s as simple as that.
And by the way, Ioannidis’ were also fixed at p=.05 or whatever value one chooses, that was Goodman and Greenland’s complaint about it, among others. Yet he gets high PPVs for unbiased tests at p=.05, decent power and no or low bias, and so do I using his equation.
You don’t know the value, but you have got a minimum for the value. That minimum is high enough to show that P values have a problem.
You say
“In any event dichotomy accept/reject should not rule in scientific inference–isn’t that we all want tests to move AWAY from? ”
I couldn’t agree more. It was one of the messages of my paper “never ever use the words “significant” or “non-significant””. I’m finding it quite hard to persuade journal editors to drop the terms, but in my view they have to go. My suggestion (similar to Goodman’s) is that one should change the words used to describe P values
http://rsos.royalsocietypublishing.org/content/1/3/140216#comment-1889100957
This hasn’t gone down well with journal editors -they are terrified that making rules like that might reduce their journal’s impact factor. That’s why I have thought for a long time that using P = 0.05 to declare a discovery has led to corruption of science. Now I understand a bit better why that’s the case.
There’s nothing scary about properly using the term “the observed difference is statistically significant at level p”.* To dislike dichotomy and then do a computation that relies on dichotomizing something that was NOT dichotomized–namely p-values–is to CREATE the problem you are then turning around and claiming we must avoid. Banning words is silly.
*I would always go further to indicate the discrepancies that have and have not been indicated with severity. The low p by itself at best tells you the existence of some discrepancy, in the direction tested. A much bigger worry is whether the p-value is valid and that requires considerations about model assumptions that you do not mention (though maybe you do elsewhere).
David, there is nothing wrong with P-values, and even a high potential FDR does not make for a problem with the P-values themselves. The problem is that people assume that P<0.05 is a licence to publish an effect as found. All we need to do is pay not attention until there has been some confirmation. Scientists should confirm their own findings with related experiments prior to publication.
False positives in drug screens are not a problem because the hits are always tested again at the next stage of the discovery programme, so your example of 1000 drug trials is not entirely relevant to your discussion. What would the false discovery rate be in your simulations if you require two successive P-values below 0.05 prior to categorising an effect as accepted? Very low, no doubt.
It would be far, far easier to get scientists to accept the fact that they should perform and report confirmatory studies than it would be to persuade them to put aside the P-values that they assume (rightly in many ways) to be useful.
The question I was asking is how should one interpret a single test that gives P = 0.047. Replication is a separate matter.
It is, in any case, pie in the sky to think that most work will get replicated. Our work on ion channels took 4 years of hard work (Lape R, Colquhoun D, & Sivilotti LG (2008) Nature 454, 722-727. Nobody will replicate it directly (though the general idea was confirmed a year later).
David, I agree that independent replication is a worthy but unrealistic goal. However you are confusing independent replication with confirmation.
I’m saying that scientists who wish to make claims on the basis of an experimental result should be required to demonstrate that they have confirmed the important result with a separate dataset. That confirmation might be direct replication, but it would be scientifically more interesting to have the confirmation consist of a related but distinct experiment that effectively tests the same ideas.
If you look at your own ion channel papers you will find many instances where there are series of experiments that reinforce each other’s conclusions. That is a useful and achievable type of confirmation. If the conclusions of your papers were found to be wrong by future work then it would several distinct statistical results that would have to have been misleading, not just one.
Yes, that’s fair enough. Important findings do get confirmed eventually during other, related, work..
The problem is that in some fields many results have failed to replicate. It would be interesting to see how many of the papers that failed to replicate were based on marginal P values. As far as I know, this has never been done.
It is certainly common for claims to be based on marginal P values. Recently a paper in Science was trumpeted in press releases and on twitter on the basis of P = 0.043. It isn’t known yet whether this was a genuine discovery or a fluke, It could very well have been a fluke, It certainly seems to me that the hubris was greatly overdone. Details are at
http://www.dcscience.net/2014/11/02/two-more-cases-of-hype-in-glamour-journals-magnets-cocoa-and-memory/
In proper uses of significance tests, they wouldn’t go to press with one small p-value, they wouldn’t hyp the result on the basis of uncontrolled studies w/o theory or mechanism (as in the glamour ones on cocoa or whatnot), and they wouldn’t tout the results based on measurements with shoddy or unverified relations to what they purport to measure as with those fMRIs. It’s not a numbers game, and it’s certainly not a science-wise error rate game; the more people try to convert it into one, the more we can expect to see spurious and silly findings. Prusiner spent a decade trying to infect monkeys with infectious prions (success rate maybe 5%), around 10 more years to be able to demonstrate it reliably, and show how prions can infect without nucleic acid. He finally get a Nobel. He has a new book out on the process, and how he was continually beaten down by rivals trying to rush into print.
David, we are therefore in agreement. FDR then becomes an argument for confirmatory experiments and for viewing the results of a related series of experiments as an ensemble rather than a consideration that should determine how P-values are interpreted.
We scarcely needed FDRs to tell us what Fisher told us from the first day: a small p-value is not indicative of a genuine effect coming just from an isolated result:
[W]e need, not an isolated record, but a reliable method of procedure. In relation to the test of significance, we may say that a phenomenon is experimentally demonstrable when we know how to conduct an experiment which will rarely fail to give us a statistically significant result. (Fisher DOE 1947, 14).
Indeed, he’s suggesting you’ve got to learn to bring it about so that you rarely fail to get significance.
But of course such rules of good science aren’t as alarming and attention grabbing as “Oh my god, if scientists do cookbook statistics, not only will each result be poorly warranted, it will show up in a large rate of unwarranted results!” To me, this is p-value reasoning showing what’s illicit about cookbook statistics. What we should be truly alarmed about are those methods that don’t let us show, by analysis or simulation, that unwarranted inferences are being spewed out, where we have to wait over a decade to discover it (as with failing to randomize w/ microarrays).
Good! We can agree at least that one cause of irreproducibility is that most people don’t understand statistics very well.
I do think though, that the people who run elementary courses in statistics must bear some of the responsibility for that. Most such courses grind through chi-squared ans t tests, and to get through the exam all you have to be able to do is calculate a t test. One has to sympathise with Sellke et al (2001) when they said
“The standard approach in teaching, of stressing the formal definition of a p-value while warning against its misinterpretation, has simply been an abysmal failure.”
Given that this situation is unlikely to change quickly, and that misunderstandings are as great among journal editors as among authors, the question is, what should be done?
My suggestion is not to specify the false positive rate for every result because that can’t be calculated. But, bearing in mind that it’s likely to be considerably greater that alpha, it seems wise that journals should discourage dichotomising results into “significant” and “non-significant” and that they should use more cautious words to describe results than is usual at the moment, perhaps something like those suggested at
http://rsos.royalsocietypublishing.org/content/1/3/140216#comment-1889100957
Perhaps this isn’t too far from your position (even if we don’t agree entirely about why)?
Well, put.
But I think David Colquhoun took it the wrong way.
Its not statistics they don’t understand, its scientific inquiry they don’t understand.
“I said “If its true, it will replicate”. That’s not quite right, I should have said “If its true, it would replicate with adequate study design and execution”.
(At least, I did not say something silly like “If it replicates its true”!)
from http://andrewgelman.com/2015/03/15/general-think-literatures-much-focus-data-analysis-not-enough-data-collection/#comment-213720
Now some understanding of statistics might spark an interest in learning about scientific inquiry.
Michael: I agree with you. There’s a danger that people with agendas and axes to grind, or who are frankly confused themselves, are having sway and creating panics, when sensible people know very well how to do good science and how to use statistical tools reliably, when they are appropriate. Test bans? word bans? How about properly interpreting and using tests and other tools? Stop cannibalizing them in backyard simulations that purport to show their dangers.
What’s a backyard simulation?!
and equally, the FDR has a straightforward frequentist interpretation. It is the proportion of tests that come close to P = 0.05 in which there is in fact no effect.
DC: I am not quite following your wording, and am not sure if your definition is same as mine. I follow Benjamini and Hochberg who say the FDR can be stated as Q = V/R where V is the number of significant (seen as positive) results from true nulls, and R is the total number of significant (positive) results (that is, from the true and false nulls) in a family of tests.
As you can see,if all of the nulls are true, Q= 1. If all of the nulls are false, Q=0. When there is a mix of true and false, Q falls somewhere in between. Since you are controlling the proportion of true nulls and false nulls in your simulation, then you are having a strong influence on the value of Q. Thus, you cannot say what FDR researchers can expect in practice when using t tests because you have no basis for projecting what proportion of their future nulls will be true. You cannot state a minimum FDR for p= 0.05 if you do not know if their nulls will be true or false, except that if they are all false the FDR will be 0. But, you might never know that they were all false.
I think the FDR, PPV and other such metrics are useful as performance metrics in validation studies as in medicine and forensics (where a test method will be applied to an individual and interpretation must be made). This work is different from the broader application discussed by Fisher, Mayo, and Lew… I concur with their points about the need to confirm results over multiple experiments/ studies. In validation studies, however, you apply a method to known samples (meaning you know the correct answer) and therefore can apply FDR and other metrics posthoc. This helps to explain method performance in simple terms and offers assurance that the method works as advertised.
Benjamini and Hochberg’s interest in FDR was to control error in a family of tests where you might never know which hypotheses were true.
Yes. It has not helped the discussion that David’s definition of FDR is not (I think) the same as in the citation classic by Benjamini and Hochberg (discussed in section 10.2.14 of Statistical issues in Drug Devlopment). No doubt he will use the Humpty Dumpty defence of his choice of terminology
http://www.quotationspage.com/quote/23101.html
Aha I confess that I hadn’t realised the Benjamini & Hochberg used the term False Discovery Rate in a somewhat different way, in the context of a different problem from the one I’m discussing. However there is no ambiguity, Right at the beginning of my paper it is defined very clearly. (I’m beginning to wonder whether some people are criticising my paper without having actually read it!)
“You make a fool of yourself if you declare that you have discovered something, when all you are observing is random chance. From this point of view, what matters is the probability that, when you find that a result is ‘statistically significant’, there is actually a real effect. If you find a ‘significant’ result when there is nothing but chance at play, your result is a false positive, and the chance of getting a false positive is often alarmingly high. This probability will be called false discovery rate in this paper.” http://rsos.royalsocietypublishing.org/content/1/3/140216
I’d be equally happy to describe it as the false positive rate (which woud have the advantage of maintaining the analogy with screening tests, It is simply the complement of the PPV but I prefer not to use PPV because it is rather obscure terminology whereas FDR or FPR are almost self-explanatory.
What is the denominator, and in what sense can the tests be a sample from a well-defined process? In a typical frequentist testing setup, you’ve got a single experiment, which can then be thought of as repeatable. This is conceptually easy. But when you generalize this to a group of experiments, immediately conceptual problems crop up. What gets repeated? Each experiment? That can’t be right, because in that case the proportion of true nulls would be fixed, depending only on the particular experiments chosen, not p(H). Perhaps the selection of the experiments is to be repeated? But at what level? Do we randomly select another 1000 drugs? What would it mean to “randomly select” drugs? Do we randomly select 1000 new diseases to test the same 1000 drugs with? New 1000 drugs? Do we randomly choose the dosage levels (assuming that a drug might be active at one dose and inactive at another)?
For it to be a valid frequentist probability, the probability must be the limit of some well-defined sampling process. There are any number of these limits in this case, and for each one p(H) will be different. And at any rate, the actual studies done weren’t part of any such well-defined process, so which you choose is arbitrary. Restricting the definition of p(H) in a proper (frequentist) way would neuter it for your use.
From a Bayesian perspective, you’ve got to imagine that you’re somehow assigned a random study, not told anything about it, and asked “Do you think this study is truly null?” It seems like any Bayesian would have trouble with that question as well.
The great advantage of simulation is that it doesn’t need much theory. You mimic real life and simply count. Counting shows that you will often make a fool of yourself if you claim you’ve discovered something on the basis of P = 0.047.
The great *disadvantage* of simulations is that without theory, they are just a bunch of numbers. In asking the reader to interpret those numbers in a particular way, you are invoking theory, like it or not. If the theory isn’t sound or consistent it doesn’t really matter what the numbers are.
True, but can you suggest any other explanation of the fact that 26% of “significant” results (those with P close to 0.047) are not real discoveries (and that’s for P(H) = 0.5: anything less than that, and the FDR is much worse). I can think of no interpretation of that apart from the one I draw, that observing P = 0.047 is a very flimsy basis for claiming you’ve made a discovery. Can you point me to an interpretation of the numbers that makes this not true?
Half of the null hypotheses are true, by your choice, and approx 1\4 of those with p-value near 0.047 are true hypotheses rejected by the test. I do not think this is surprising. Try it again with 80% of the null hypotheses true and the FDR should be much higher, right?
Yes of course if P(H) is less than 0.5, the FDR increases. That’s why I describe 26% as a minimum FDR. If P(H) = 0.1, the FDR is 36% (if you use P=<0.05) and 76% if you look only at P close to 0.05. Both are disastrously high.
There’s only one reasonable interpretation, and that is an application of Bayes’ theorem with p(H) a subjective probability of a given study’s probability of being not null. Very simple. But that has no effect on anyone except a subjective Bayesian with that p(H). The problem is in making the interpretation more general than the almost trivial subjective interpretation. (Just to emphasize, I’m fine with the subjective argument, but you’re making a more general argument here: you wouldn’t have had to invoke “mimicking what’s done in real life” if you were just making a subjective argument…)
Nothing on earth will make me happy to use subjective probabilities!
David, surely you would consider your own subjective prior on the effectiveness of a homeopathic remedy to be superior to the prior that might be assumed by a chiropractor, for example. I suggest that you use subjective Bayes all of the time for inference. You just don’t formalise and report it.
Yes, I’m being a little naughty here. However, to reject Bayes as strongly as you do and to make it sound like it is a rejection of Bayes for all purposes is not appropriate in my opinion.
I agree, but I wasn’t dealing with groups of experiments, but the simpler question of how should one interpret the observation of P = 0.047 in a single experiment.
It’s obvious that P(H) will differ if you do a different sort of experiment. So will the P values. So one can say little about lifetime error rates. That wasn’t the question that I was asking.
If that’s what you’re doing, then p(H) only references a single experiment (and its theoretical replications), and the frequentist probability p(H) is 0 or 1 (since the null is either true or false). It doesn’t seem like that’s what you were going for; you *must* have had groups of experiments in mind, because its the only way to get a nontrivial probability for p(H) (in some experiments, the null will be true, and in others, it will be false).
Alternatively, you can interpret this probability in a Bayesian manner about a single experiment, and p(H) can be whatever you like, but you’ve metaphorically cut your legs out from under you because your argument is purely Bayesian.
Richard: The truth is that H is forced to change in the argument. It is at one point a specific hypothesis whose truth is not the result of a random experiment; at another point we have an experiment of drawing hyps from an urn with an imagined known proportion of “true” hypotheses. Then it’s truth can be seen as the result of a random experiment, sort of. This illicit switching is standard in these arguments which have been around for decades. As a statistical hypothesis H assigns probabilities to outcomes; as a result of a random trial it no longer does.
One example that comes to mind on this blog is Isaac and his college readiness, depending on whether he came from Fewready or Manyready town. The data are his high test scores.
Only a Bayesian would say P(H) = 0 or 1 and I am not a subjective Bayesian.
In screening tests P(H) is the prevalence of the condition being tested for in the population you are testing,. It isn’t 0 or 1 but a perfectly well-defined frequentist probability.
In a directly analogous way, in the case of significance tests, P(H) is the probability that there is a real effect. That’s harder to estimate then the prevalence of an illness, but it’s exactly the same sort of probability and it isn’t 0 or 1 (well, OK it might be 0 for a test of homeopathic pills, but not in general),
Furthermore my conclusion is not sensitive to the fact the P(H) isn’t known. Even when P(H)=0,5, the false positive rate is a disastrous 26% and smaller values make it even worse.
David: For a statistical hypothesis (not the result of randomly selecting a hypothesis from a barrel of hyps) regarded as true or false, it is correct to say that the only probability a frequentist would give it is 0 or 1. It’s the subjective Bayesian who would give it an intermediate value, depending on how strongly they believed its truth or (for some) how much they’d bet on its being true. I have a feeling you’ve been fooling with* (*meaning: spending time with”) FDRs and screening so much that you’re thinking in those terms. An empirical Bayesian, if there was some kind of frequency with which certain parameters occur, might also give it a frequentist prior. Neyman’s idea for a frequentist prior for, say, a particular person, say Mary, having a disease, might allude to a combination of genetic and biological factors thought to bring about the disease. Reichenbach’s frequentist was a man of the future, according to Reichenbach himself. That is, he thought at some point in the future scientists might be able to judge the type of hypothesis that would be true with some frequency, but even his student Wesley Salmon thought that rather far fetched. In some cases though, knowing how it was constructed, e.g., by ad hoc means, might be a clue–but this just boils down to an assessment of its warrantedness by the data, not it’s probability. (Not the same thing.) Then I spoze there are possible worlds. I just don’t see why we’d want to use the % of world’s where a law or claim held as grounds for assigning a prob to it in this world, even if by some means we were able to find it out. So anyway the standard view for a fixed parameter or stat hyp is indeed a prob of 0 or 1.
I’m very sorry that you regard the analogy with screening tests as “fooling around”. The screening problem is very important for human welfare.
The problem seems to be the word “Bayesian”. The very mention of the word divides statisticians into waring camps. I, as an experimenter, would scarcely dare to enter the battle if it were not for the fact that many statisticians agree with my views just as strongly as you seem to disagree with them.
I maintain that I am doing no more than to apply the standard rules of conditional probabilities and see no necessity to mention Bayes at all. That is undoubtedly the case for screening tests and I maintain that it’s also the case for significance tests.
At the risk of repeating myself, I simply can’t understand at all is why you are so unwilling to accept the results of simulations. They simply mimic what everyone does in real life and they show unambiguously that P values don’t answer the question that experimenters want to ask. You keep saying that you don’t like this approach but I still can’t understand what you think is wrong with it.
David: I was giving a generous interpretation of your gaff about 0, 1 probabilities–instead of just saying you’re flat wrong– I guess you didn’t see that. I didn’t say fooling around, just fooling with. I will change the phrase to what I meant, merely “spending time with”. Your spending time with the PPV measurements might have made you so used to talking that way–I was generously suggesting–, when in fact Richard was correct in what he said about frequentist assignments.
David: As a resident Bayesian gadfly ’round these parts, let me just chime in and say that when you write, “Only a Bayesian would say P(H) = 0 or 1” you are, as Mayo says, flat wrong; and when she writes, “For a statistical hypothesis…regarded as true or false, it is correct to say that the only probability a frequentist would give it is 0 or 1,” she’s right.
You seem very confused as to what statisticians (frequentists and Bayesian alike) think you’re doing when you perform your simulations and generate your FDRs.
David: The lump of .5 on the null is scarcely unbiased.
Casella and R. Berger (1987) show that “concentrating mass on the point null hypothesis is biasing the prior in favor of H0 as much as possible” (p. 111) whether in 1 or 2-sided tests.
Here’s their paper:
Click to access casella%20and%20bergernocover.pdf
Here’s my post on this.
Richard: I agree with you here as regards the ill-posed measurement, which isn’t to say it couldn’t be restricted, but why restrict it in any one way? This is still not my gripe but very relevant.
The difference between P=P’ and P,<= P' is well known. In the former case, in a Bayesian framework, large trials give less evidence agains the null and in the latter case more. This is easily explicable in terms of likelihood. See Chapter 13 of Statistical Issues in Drug Development
http://www.senns.demon.co.uk/SIDD.html
especially sections 13.2.8 & 13.2.9
It is becaus if alpha and beta are type I error rate, then (1-beta)/alpha is monotonically increasing in the sample size. However,. L1(P)/L0(P) is not.
Stephen: Finally I have the chance to directly connect with you on this one point! The point of my recent post about what’s wrong with using (1 – beta)/alpha as a likelihood ratio is relevant.
Indeed, the issue deserves another one of your analogies to what Jeffreys said (about tail areas), which I see is quoted in your post (I missed it at first). Let me explain the issue I’m now on about.
If you use the power/size ratio as a likelihood ratio –which is NOT how they are to be used in tests, you wind up being able to say that taking tails into account gives more evidence against Ho in favor of an alternative point hypothesis H1. It’s Pr(P<p'; H1) that's doing the damage. This is either power or the P-distribution under H'. But neither are "fit" measures, neither should enter the computation as a likelihood or LR.
Using the error probabilities as likelihoods in a Bayesian computation gets things reversed!
This is connected to what you call (rightly) the nonsensical, and a bit later, the ludicrous in your drug development book (p. 202.) I know you will say the above point, which is my main one, is rather different, but if you think about it for a bit, you'll see the connection. Anyway, as regards my main point, do you see why I say it calls for an analogous type of expression? (let me know if you invent one.) Looking at tails never gave more evidence against when used in significance tests as intended, only when used as unintended (in forming "likelihood ratios" for a Bayesian computation).
I am not necessarily defending (1-beta)/alpha as a way to look at things. Note that David Colquhoun’s argument is mainly about exact P-values and for that it is L1(P)/L0(P) that is relevant.
Stephen: But those are still tails, yes? The same holds for them.
Not really. If I were to replace P the tail area by PD the probability density then L1(PD) would equal L1(P) and L0(PD) would equal L0(PD) so I am not sure what the “same” is that holds for them. The inferences are quite different.
When I have alpha I know that the PD applies to a statistic in the area defined by alpha but I don’t know where. When I know P i know exactly what the PD is.
Stephen: I will have to write to you on this later. Sorry not to be able make my query clearer here.
WordPress just notified me that we’ve hit an all time high in the number of views with this post, and there are 4 more hrs to go in the U.S. Many thanks to Stephen.
That’s good. I’ve been busy inviting my 10k twitter followers to contribute to the discussion. Some may have looked, though if so they’ve been sadly silent!
I am pretty sure that is the power of David Colquhoun’s twitter following augmented by his formidable blog that is responsible for the large number of hits. So, many thanks, David!
Here is a way of defining a p-value for a single data set
x_n. The null hypothesis corresponds to a stochastic model
P_0. The p-value is based on a statistic T. Given T, P_0 choose a number
alpha which specifies what is meant by typical, that is 100alpha% of
data generated under P_0 are typical. Given alpha specify a region
E_n(alpha) such that T(X_n) lies in E_n(alpha) with
probability alpha for data X_n generated under the model
P_0. These are the typical values of T(X_n) under P_0. The value
T(x_n) for the real data is typical for the model P_0
if T(x_n) lies in E_n. The p-value of T(x_n) is p=1-alpha for the
smallest value of alpha such that T(X_n) lies in E_n(alpha). Thus a
p-values is a measure of how well the model P_0 can replicate the
observed value of T(x_n). There is no mention of any generating
mechanism for x_n, the definition is neither Bayesian nor
frequentist. If the p-value is small then a weak definition of
typical is needed to make T(x_n) typical under the model. Thus the
p-value is one measure of how well the model approximates the data. If
the approximation is poor, that is, the p-value is small, one can try and
find reasons for this such as outliers, bias, manipulation of the data
but also the choice of T and P_0. In general T should be smooth and
P_0 bland to make the analysis stable under small
perturbations. There can be no likelihood based concept of
approximation and so its role is limited to discrete models where
likelihoods are non-zero probabilities.
lauriedavies: I’d say that this is “frequentist”, although not in the sense that it postulates a frequentist mechanism as “underlying truth”. It is however frequentist in the sense that what you say implies that we think of P_o in a frequentist way. It is about measuring to what extent a frequentist mechanism P_o (which is a human idea, not a “natural truth”) approximates the data in the sense that the data look typical under P_o.
I’m of the opinion that if one is going to use p-values, that a study that follows the scientific method should always conclude with a high p-value, not a low one. Why? Because that means at the end of the study there is a working model for the generative process underlying the data that can be further validated / invalidated by future studies.
that’s one thing that is appealing about ending with a posterior distribution in a bayesian analysis. implicitly the posterior distribution also defines a distribution of generative models consistent with the data and usually more specific than the distribution of generative models before obtaining data.
These may turn out to be right or wrong, but without putting forth any kind of hypothesis about “what is” (ending an inquiry with p<.05 only says "what isn't", and even then under particular circumstances), it's hard to make progress.
vl: It’s part of an inferential process that asks specific questions in pieces in the process of arriving at a model that adequately captures the data generation or whatever the question is. Unless one were asking an extremely local question, as with testing assumptions of statistical models–for which p-values are just right–there would be an alternative inferred on the basis of a low p-value, so we’d say more than “there’s a genuine effect” (although that’s a good start).
A large p-value usually only allows deeming some aspect of the model adequate, estimation or a set of severely passed values goes further. Although failing to reject nulls has been (substantively!) informative in physics, e.g., equivalent principle.
But the big difference with the Bayesian goal is that we are using statistics to evaluate how well tested or warranted claims are. That is very different from how “probable” they are. Most interesting theories, models, causal claims are not considered “probable’ in any formal sense; but we can often actually detach or infer claims, using the statistical properties of the method to qualify the claims inferred. This is more nearly what we do in ordinary inference and learning which is not of a formal statistical variety, e.g., Valtrex gets rid of herpes sores in around 1-2 days; 6-year old Mary reads at at least the third grade level; prions (the cause of mad cow and many other diseases) infects without nucleic acid, falsifying what had been a fundamental principle of biology.
I’m sympathetic to vl’s point here and think it would be a good shift in emphasis – relative to pure p-values – to put modelling generative mechanisms first, followed by model estimation and model criticism*. That way silly theories would have a harder time getting off the ground in the first place – one could always ask ‘so what’s the proposed generating mechanism here?’ before proceeding.
[Admittedly there are probably subtle questions to do with establishing the existence of some ‘effect’ without having an explicit model, but in general there should be *some* model which is being used to interpret the effect, even if it is not very detailed or well-understood. This would just underscore that interpreting the effect is relying on some unclear model.]
In this approach one should at least end with an improved generative model, along with an assessment of its adequacy (are the data in hand ‘typical’ compared to those generated from the new model) and its ‘reasonable’ parameter values (probability, likelihood, confidence, severity level etc).
So, Mayo – taking this approach wouldn’t typical modelling-oriented frequentists and bayesians set up essentially the same generative model (here parametric/likelihood-based say, despite Laurie Davies’ interesting points) and simply use slightly different estimation methods within that model (Davies’ ‘act as if true’, Box’s ‘estimation’ c.f. ‘criticism phase etc etc). Spanos’ approach (and co-opting of De Finetti’s ideas) doesn’t seem that different to say Bernado’s or Gelman’s approach, just that the latter use bayes for estimation and also integrate over the parameters when generating predictions for future values, while Spanos uses frequentist estimation methods and would choose some fixed parameter value or range of parameter values (presumably?) for generating predictions.
In this vein – regarding the Mary example (similarly, I think, Issac’s ‘readiness’ as in one of your other examples), and without thinking too carefully, why not set up a generative model predicting test scores on the basis of some parameter meant to capture ‘reading ability’ or whatever. Then do parameter estimation within that model (assuming model checks of adequacy/misspecification are performed before/after). Both bayesian and frequentists rely on the adequacy of the model but, assuming this is established, both estimate a parameter value in a generative model. The impact of the prior – i.e. any regularisation – can of course be assessed, as is standard ‘best practice’ in the applied bayesian literature. Similarly the impact of any other modelling assumptions.
By re-stating the problem as one of estimation within a generative model I don’t really see any major controversy? Perhaps I am wrong? It also seems to nicely shift emphasis away from ‘strawman null’ stuff. Are there specific examples you can give where both set up the same generative model, the bayesian uses ‘nice’ priors (smooth etc) over the parameter space and they come to very different conclusions. (Similarly for the likelihoodist).
*I should acknowledge Laurie Davies’ interesting points regarding *not* separating things into ‘get model’ then ‘act as if true’ phases, but I’m also a bit unsure about a) how to connect this approach to an underlying scientific theory which (say) is expressed in terms of parameters and b) whether the ‘two step’ approach of determining model adequacy and then estimating parameters within a model cannot be saved by various forms of ‘robustifying’ the standard approaches.
Laurie:
I do agree that likelihood as it is often defined mathematically is a disaster/embarrassment.
Mike Evans instead defines posterior/prior as the more relevant definition of evidence (and the topology is _trapped_ to being finite, as all observations simply are.)
Additionally, my sense is, John Copas’ work on envelope likelihood (Likelihood for statistically equivalent models JRSSB 2010.) which had similar motivation (inference for all models consistent with the data) has not yet gotten very far?
(Sorry if this seems rather technical – it is – but its also interesting to some of us.)
Personally I vote for a guest post on this topic from Laurie (or someone else connected). I bought his book but would be great to have a blog discussion too, especially for those like me looking to use statistical tools but coming from different backgrounds.
To go off topic, I’d like to point out that my real job has been maximum likelihood fitting of models to recordings of single molecule activity (an aggregated Markov process with discrete states in continuous time). This allows us to estimate up to 18 free parameters In favourable cases. See
http://www.onemol.org.uk/?page_id=175#chs96
and
http://www.onemol.org.uk/?page_id=175#chh03
In this case the models are based on postulates about the physics of the process, so they differ from the sort of empirical models that are common in statistics.
From time to time, I’ve tried calculating likelihood ratios in an attempt to distinguish between rival models, but they always seem to give tiny P values, even for fits that are indistinguishable by eye. I’ve never quite understood why this is, though it could be because the parameters are often on the edge of the parameter space so the usual chi-squared criterion is inadequate. Perhaps, more importantly, systematic errors could contribute too. As a result I’ve hardly ever published the results of likelihood ratio calculations. And still more rarely have I published a test of significance. They just don’t seem to be very trustworthy.
David, on the topic of comparing models using likelihood ratios: you can’t. Likelihoods are defined only to a multiplicative constant, and that constant is almost always unknown and is affected by the model. Thus likelihood ratios don’t work when the likelihoods in question come from two distinct models. The also don’t work when they come from two distinct likelihood functions. The restrictions on what one can do with likelihoods are several, but the failure to notice them is what I believe underlies almost all of the anti-likelihood feelings that you will read in this blog and elsewhere. It is also responsible for at least a couple of alleged ‘counter-examples’ to the law of likelihood.
Well I was following Rao’s method and, I should have mentioned that the mechanisms (models) being compared were nested (one was a subset of the other). But I still couldn’t trust the results.
In the case of single molecule records, the data a sequences of open and shut times so the data come as distributions -that makes ML estimation very attractive (because you observe the distribution, rather than merely assuming something convenient
In my humble opinion David’s considerations on FDR are correct if you consider the interpretation of a p-value taken from a series of papers investigating different hypotheses (some true and some wrong). So they are correct if you look at the problem from the point of view of a reader.
In the analysis of a trial, the scenario is different, the trialist is assessing a single hypothesis and the corresponding alternative . When multiple hypotheses are tested it’s a multiplicity problem and that’s another story.
The single hypothesis could be true or wrong, obviously you don’t know this in advance and a Bayesian may apply a prior, but this does not mean that the hypothesis is true x% of the times and wrong (100-x)% of the times. It simply means that he/she is more/less prone to believe in one hyp. vs the other.
So from the point of view of a trialist I can’t see any reason why he/she should adjust the analysis taking into account all the investigations performed on the earth assessing any kind of hyp.
Similarly, to me, the difference between a screening and a clinical trial is that during a screening a diagnostic test is applied to a population with some subjects with the disease and some without (with an unknown mix), in a clinical trial a test is applied to assess an hyp. which could be true or wrong. The p-value is derived assuming that the null is true. Its information is not misleading, too conservative or too liberal it simply ‘does exactly what it says’.
Thanks Paolo!
I agree. P values do exactly what they claim, but sadly that isn’t what we want to know.
It would help if people distinguished actual from “computed” or “nominal” P-values. According to this article by Benjamini, Ioannidis downplays or ignores them (although one would have thought they would fall under his broad umbrella of ‘bias”).
“Simultaneous and selective inference: Current successes and future challenges” Yoav Benjamini
Biometrical Journal 52 (2010) 6, 708–721
From Benjamini:
“I would like to turn your attention to the paper by Ioannidis (2005) ‘‘Why most research findings are false’’. This paper has generated a wave of responses, both in the scientific press and in public debates (see Boston Globe op-ed of July 27, 2006, at http:// http://www.boston.com/news/science/articles/2006/07/27/science_and_shams/). …… To a reader of the paper who is familiar with Multiple Comparisons it is clear that the source of the problems he is discussing is the use of nominal hypothesis testing even though many hypotheses are being tested, both within and across studies, and manifested via publication bias. In fact Ioannidis is repeating the very same arguments that were brought up by Soric- (1989), where he calculates the expected number of false claims as a proportion of the claims made. Neither the work of Soric-, nor the FDR concept and the large body of methodology it generated is recognized. In fact multiplicity is discussed in passing by Ioannidis, as an irrelevant issue to his concerns. Ioannidis is not an isolated voice that ignores the multiplicity problem in medical research. An editorial discussing the Hormone Therapy study of Women Health Organization (Fletcher and Colditz, 2002) states: ‘The authors present both nominal and rarely used adjusted CIs to take into account multiple testing, thus widening the CIs. Whether such adjustment should be used has been questioned,’ I was surprised by these claims. ”
Soric, B. (1989) Statistical ‘‘discoveries’’ and effect size estimation. Journal of the American Statistical Association, 84, 608–610.
Mayo, you are not the only one who tries to distinguish between ‘nominal’ and ‘actual’ P-values, but to do so without being explicit about why the different types of conditioning are desirable is not helpful. Further, I don’t think that ‘P-value’ is a concept that demands a particular conditioning and so the word ‘actual’ is misleading.
I think we would be in a better position with P-values if we just allowed them to be data-based summaries of evidence (even though they are inferior in that regard to likelihood functions!) and then demanded quantification of the influence of the methodological aspects that would lead to differences between ‘nominal’ and your ‘actual’.
No one view of statistical correctness can own ‘P-values’ at this late date. To insist otherwise is to make the job of understanding the relationships between statistics and scientific inference even harder.
Thanks very much for the Benjamini and the Soric references. They illustrate why I chose to address the question: how should you interpret a single observation of P = 0.047. One big problem with multiple comparison corrections is how to decide which tests to include, All tests in one ANOVA? All tests in one paper? All tests in one project?
But from the point of view of finding a minimum false positive rate, the frequent occurrence of uncorrected multiple comparisons can only make the P value even more unreliable than I allege.
David: There’s something very important that you don’t yet understand. It is not a sign of unreliability of the p-value (or other error probability, and I certainly don’t mean to raise p-values above other and often more relevant error probabilities) that nominal (computed) p-values often differ from actual ones as a result of selection effects, biases, failed assumptions, cherry-picking, multiple testing, post-data subgroups, stopping rules, double counting. It is a sign of the capacity for reliability and error control offered by the overall error probability approach. It is a sign of strength. In fact it is their chief asset (as compared with rival approaches).* The central difference between error probability approaches and those non-sampling approaches is that on the error statistical approach, the import of the data is not independent of the capabilities of the method to control and reveal the approximately correct–and the wayward–error properties of the method at hand (for the given data generation, data and hypothesis). We don’t “condition” on the actual data which would preclude the sampling distribution (once the data are in hand) and thus would preclude error probabilities. This central difference is why we cannot obey the likelihood principle that is embraced (or follows from) non-error-statistical approaches. Not that violating the LP is sufficient for error control but it is necessary.
The capabilities of methods to control and inform us of the actual capability of a method to have avoided misleading interpretations of data (wrt the problem at hand) is not a fallibility but a crucially important asset. It’ easy to demonstrate, for example, that reporting the 1 stat sig result of 20, while ignoring or burying the 19 non-significant results, results in an error probability of ~.64 (assuming independence, but clearly not small). To wish to replace error statistical approaches with any approach that is unable to directly pick up on and reveal what is causing the distorted error probabilities, is to give up on error control.
The only thing noteworthy about what Benjamini reports (and I will investigate exactly what’s behind it, I hadn’t read this before) is that it reveals a very serious blindspot in Ioannidis–perhaps he’s since corrected it.
* By the way, the science-wise PPVs are not the same as the error probabilities that are relevant for interpreting a specific inference to this hypothesis. But the bad results of an Ioannidis depend on these selection effects, biases, significance cheating, or (postulated)poor prevalence of “true” effects. I would much rather that the reported error probability reflect the actual crime. Some selection effects, even double counting, stopping rules, etc., while prima facie altering (raising) the error probabilities, may be able to have the bad error probabilities overrided by subsequent checks. So far as I can tell, Ioannidis’ punishment numbers for “bias” are not connected to known alterations of error probabilities through multiple testing, stopping rules, post-data subgroups etc. So far as I can tell, they are numbers he arbitrarily assigns and are not calibrated against known altered error rates . As Goodman and Greenland point out, he will often punish a case both by raising the type 1 error probability AND lowering the prevalence of true effects in the field. It’s much better to pinpoint the actual methodological sins committed and try to evaluate their impact on the reliability of the specific hypothesis inferred, than to promulgate the kind of guilt by association seen in his charts.
You say “There’s something very important that you don’t yet understand. It is not a sign of unreliability . . .”
I didn’t say that P values are “unreliable”. I said that they don’t measure what an experimenter wants to know, namely the probability that they’ll be wrong if they claim to have discovered something.
‘Prob of being wrong in claiming to have evidence for H’ is ambiguous; the prob that THIS H is wrong is rarely meaningful (0 or 1), but the prob they’d have produced results more discordant from H— say that the deflection of light is ~1.75″–, than those they’ve brought about from radioastronomy, i.e.,x, under the assumption that H is false (the deflection is closer to the Newtonian value .87″) about the data generating mechanism will be very low (if they’ve done things correctly). This prob does not refer to other H’s some other people in other sciences or other times might have tested well or badly.
But we’ve already seen that you’re inclined to use a diagnostic screener’s notion of “prevalence of true H’s in an urn of H’s”, which does not give you the relevant error probability for H-on the deflection of light.
(It’s not really even an error prob in the sampling theorist’s sense; this always refers to the sampling distribution of a statistic over other outcomes).
You can restrict your focus to diagnostic screening, but will be overlooking what makes error probs work, or not work, in the case at hand.
Talking of light, it’s one of the classical examples of the hazards of P values that for many years each new estimate of the speed of light was outside the confidence limits on the preceding estimate (though, admittedly, that might be a result of systematic errors rather than anything more subtle).
I think that there is a subtle difference between trying to calculate the probability that a hypothesis is true (pure Bayes) and calculating a lower limit for the fraction of times that you’ll be wrong if you claim you have made a discovery on the basis of a P value. It’s the latter that I’m trying to do.
I’m not pretending that you can get a science-wide error rate, but if each individual test has a larger false positive rate, that’s sufficient to show that there’s a problem, It’s obviously true that each sort of thing you test will have a different false positive rate, so when thinking about a single test you have to imagine its a sample from a large number of imaginary repetitions. That’s a very standard procedure in statistics and it doesn’t seem to raise any particular problems in this case.
Simulating what almost everyone does in real life shows very clearly that you’ll get a fraction of false positives that’s a lot higher than most non-statisticians expect. Furthermore, the results of simulations agree quite well with the results of the quite different approach taken by respected statisticians such as Berger & Sellke, and by Valen Johnson.
In order to refute my conclusion, you have to say that the way that most people use t tests is wrong, or there is something wrong with the way I’ve done the simulations. I wait with interest.
“detach or infer claims, using the statistical properties of the method to qualify the claims inferred. This is more nearly what we do in ordinary inference and learning which is not of a formal statistical variety, e.g., Valtrex gets rid of herpes sores in around 1-2 days; 6-year old Mary reads at at least the third grade level; prions (the cause of mad cow and many other diseases) infects without nucleic acid, falsifying what had been a fundamental principle of biology.”
With this approach, one will never build up an understanding of how Valtrex actually works. The reason is because systems in general have conditionality and non-linearities built into them. At some point in one’s understanding you have to switch from a pointillistic view of knowledge to an integrated one. There’s not enough statistical power in the universe (or money for clinical trials) to make scientific progress if one keeps detaching knowledge in this piecemeal way.
Regarding the criticism of the “screening” view. The separation of a large-scale screening concept from any other scientific inference seems wholly artificial. Scientists care about being right or wrong. It matters if your result is one readout of a screening assay of 6000 measurements. It also matters if your result is one publication out of a 6000 paper literature. Sure, power and the range of uncertainty that’s unacceptable may vary, but the objective is the same in either case. Simply put, how often you’re right or wrong about an inference matters.
I think DC has only discovered what happens when you run a simulation that way. The setup regarding % true nulls cannot be taken as representative of any real situation I am familiar with. The simulation does not permit one to interpret what should be a minimum FDR for our future use of p-values. One of the problems is thinking “truth of null hypothesis” is a random variable, as Mayo discussed. That does not reflect research practice.
I recently simulated comparisons of bone sizes (t tests) from different people and from same person (such as right arm vs left arm). I knew of course which null hypotheses were true or false and was able to get an actual FDR from the results of close to a thousand tests per experiment. IF my reference data are representative of the population from which future forensic cases will be randomly drawn, then my results might give us insight into future FDR across many case applications. But each case is different, and when comparing bones from two people of vastly different size, there are typically no false positives (or false negatives) but if two people are nearly same size then we expect false positives to be a concern but really worry about the false negative. The latter worry renders the method inconclusive in this circumstance.
The point is the error probability for the single test when it is really only a single test is effectively represented by a p-value. And there is severity. Keeping in mind that my simulation was not imaginary nulls but based on real data and meaningful tests (with the false nulls created by random pairings), it is interesting to note that my FDRs were less than 5%. The false positive rate was close to alpha for all but one bone.
A notable point is that the % true nulls was typically only 10%, more or less. As I have noted previously, this was controlled by my study design and affects the FDR. However, I was conservative in the sense that when bodies of people are commingled and you wish to compare all lefts to all rights for a given bone, the number of pairwise comparisons rises exponentially with number of people. Thus, the number of false nulls will greatly outweigh the true nulls.
My study is different from DC, but I do not believe one can state what the FDR will be is future research nor conclude there is anything like a disaster based on his study. I might be able to make such an assertion from my study if I could convince you that my reference data is appropriate for the applicable reference class (future forensic cases).
John: I really like your commingled bone remains example, and now that I’m in one of my own libraries, I have a copy of your book! Will read the comments more carefully tomorrow; the ferry to Elba has made me seasick.
Out of touch for the next 8 hours.
As a molecular biology student grappling with biostatistics at a novice level this post/comment thread is a very welcome but steep learning curve!
Thanks to you all.
Commenter “Paolo” provided the clearest explanation (to me at least) as to where the crux of the debate resides, saying “…the difference between a screening and a clinical trial is that during a screening a diagnostic test is applied to a population with some subjects with the disease and some without (with an unknown mix), in a clinical trial a test is applied to assess an hyp. which could be true or wrong. The p-value is derived assuming that the null is true. Its information is not misleading, too conservative or too liberal it simply ‘does exactly what it says’.”
So, “if the false discovery rate is [for e.g.] 70%, the PPV is 30%” & a p=0.05 indicates that “there is a 5% chance of seeing a difference at least as big as we have done, by chance alone”, doesn’t each statistical measure fill in their own section of the statistical picture – without redundancy? It seems that the p-value is not THE problem, but simply the end stop of where all data interpretations problems come up against.
[Reference: “An investigation of the false discovery rate and the misinterpretation of p-values (Colquhoun, David)”]
So in the context of biomedical research – wouldn’t the reliablity of the p-value largely hinge on the degree of ‘fit’ with prior assumptions made on the magnitude of effects within a particular sample size?
Apologies if my novice level is all too obvious and/or causes painful face-palms.
Suppose the test statistic T is the standard t-statistic and the P_0 of the null hypothesis is N(0,sigma^2). The sample size is 10 and the attained p-value is 0.047. Some questions arise with hypothetical answers. (Q1) Why use the standard t-statistic? (A1) The model is the normal distribution and the t-statistic is optimal. (Q2) Why the normal model? (A2) The data look normal. (Q3) The data also look Laplace (double exponential – for a sample of size 10 there is little hope of distinguishing them). What to you do if you accept this model? (A3) Use the maximum likelihood estimators, the median and the mean absolute deviation. (Q4) The Laplace p-value is 0.025. Which one do report and why? (A4) ? (Q5) Your data contained two rather largish values. What did you do with them? (A5) I used the Grubbs’ test and everything was alright.
omaclaren: Thank you for your interest. Huber `Data Analysis: What can be learnt from the past 50 years’ states on page 94, ` … statisticians have become accustomed to act as if it were true’, it here being the model. I dislike the separation of EDA and so called formal inference. In particular I dislike the switch from the weak topology of EDA to the strong topology of formal inference. The two are connected by the pathologically discontinuous differential operator. Trying to do statistics whilst at all times treating models as approximations is work in progress. I don’t have a `magische Freikugel’ unless it is perhaps the seventh.
Keith O’Rourke: thank you for your comments. I confess to not being well acquainted with the literature. I will look at the work you mention. My feeling for `consistent with the data’ is that any such concept of consistency in the sense of goodness-of-fit will be based on Vapnik-Chervonenkis classes. Vapnik has written something on this but the reference escapes me.
David Colquhoun: Likelihood is a very bad way of comparing models. Your problem with goodness-of-fit looks similar to an example in Chapter 5.4 of Huber `Data Analysis’, an excellent book by the way.
Howell Tong is organizing an anti-likelihood workshop in Warwick
http://www2.warwick.ac.uk/fac/sci/statistics/crism/workshops/non-likelihood
Andreas Buja is working on approximate models
Click to access Talk-ETH-2014-11-25.pdf
I also gave a talk at the same conference but having no home page you will have to contact me at
laurie.davies@uni-due.de
to get a pdf-file
Well, maximum likelihood certainly give pretty good estimates of the the parameters, and that’s what matters.
Click to access c-hatton-hawkes-03.pdf
It’s a side-issue but I would just like to draw attention to the fact that diagnostic screening should not necessarily be thought of in terms of specificity and sensitivity for reasons given by.
1. Dawid AP. Properties of Diagnostic Data Distributions. Biometrics 1976; 32: 647-658.
2. Miettinen OS, Caro JJ. Foundations of Medical Diagnosis – What Actually Are the Parameters Involved in Bayes Theorem. Statistics in Medicine 1994; 13: 201-209.
3. Guggenmoos-Holzmann I, van Houwelingen HC. The (in)validity of sensitivity and specificity. Statistics in Medicine 2000; 19: 1783-1792.
Basically, false positive rates are not independent of prevalence. On the other hand, ironically, type I error rates for a correct hypothesis test are independent of the probability of the null hypothesis being true (assuming one admits such a cocept).
Stephen:
I will look up these papers, curious what they replace them with.
Why is it ironic that type 1 error rates are independent of the prob of the null being true? That is how they were designed deliberately.
It is ironic because the screening analogy works better (albeit still imperfectly) for hypothesis tests than it does for screening.
“Basically, false positive rates are not independent of prevalence.”. Given that the simulations discussed involved t-tests, can we add to this that the false discovery rates will be additionally affected by “how untrue” the untrue hypotheses really are?
John: not on the dichotomous view used in these types of criticisms of tests. That’s why it is hard for Ioannidis to empirically justify his results. In real life, scientists look at magnitudes, and (hopefully) don’t claim to have evidence of a genuine effect based on a single p-value attained from p-hacking no less. These criticisms have some bearing on science-wise screening activities, which spew out “interesting” genes from high throughput screeners, and that was their initial target, but not scientific inference. The worst part isn’t the unwarranted caricature, it’s (a) creating further confusions between error rates based on a sampling distributions (as in N-P and Fisherian tests) and posterior probabilities or posterior prevalence rates; (b) resulting in recommendations that scientists study effects already known to be true or nearly true in order to get good rates in some long-run; (c) failing to identify the actual sources of any specific, poorly tested claim, and conversely, failing to identify a well tested effect in a field that happens to have had a poor rate of successful attempts so far. (Guilt and innocence by association.)
Taking this attitude seriously, maybe we’ll see “retraction rates” traded amongst journals like carbon emission credits.
I’m not opposed to attempts to apply assembly-line techniques to reduce the overall “noise in the network”, but the most effective means would be by encouraging/insisting on responsible science.
I understand the problem with collapsing everything into dichotomous metrics. I think it has a limited purpose in describing how a method performs, but much less in interpreting a specific result. However, following on Stephen’s comment about dependence between false positives and prevalence, I am noting that in our simulations the FDR will also be affected by the effect sizes of the false nulls we choose to include. How does one make a claim the the effect sizes of the false nulls in a simulation are representative of (all?) future research applications?
I agree. However, in David’s simulation he declares the null hypothesis by fiat.
In my view, however, this does not mean that he is calculating the probability that scientists actually make a fool of themselves. He is calculating (i think) the probability of a scientist making a fool of him or herself IF a scientist decides a null hypothesis is false and IF this decision is based on p just less than 0.05 and IF the only way that H0 could be true would be by the effect being zero.
This is not, of course, an actual probability of making a fool of oneself since a) it may be that P-values close to 0.05 are relatively rare b) one can make a fool of oneself by failing to spot a false null hypothesis c) the proportion of true effects that are exactly zero (rather than. say, worse than useless) may be small d) scientists may accept that mistakes are inevitably common and not shout ‘you fool’ every time somebody makes one.
Good -now we are getting somewhere.
I’m quite happy to admit that you points (a) to (d) are perfectly right. Indeed some of them were dealt with in my paper. Of course some P values are much smaller than 0.05 and that isn’t a case that I investigated. But quite a lot of reported values are actually in the range 0.01 to 0.05, and anything in this range is used to claim that a discovery has been made. And that includes the glamour journals (I cited an example from Science earlier/
It’s true that if you don’t use a point null then you can get a different answer. But the fact is that everyone does use a point null -largely because that’s what they are taught to do in introductory stats courses and textbooks. I remain to be convinced that it’s a silly thing to do, but that’s beside the point. It is what people actually do, and that’s what I was mimicking.
“…the fact is that everyone does use a point null -largely because that’s what they are taught to do in introductory stats courses and textbooks”
However
a) These are the very same books that teach them to calculate p-values, which you now regard as a mistake, So it seems to me to be strange that you cite such books as a defence of your point null.
b) This still has got nothing to do with true error rates in asserting hypotheses. At best even if scientists really believed that what they were testing was point nulls it would point to an inconsistency in their behaviour. This is not directly relevant to the true false positive rate
c) This point is exactly one on which there is strong disagreement. History seems to suggest that for more than a century and a half from Bayes to Jeffreys scientists did not do this (or at least not in the way that J Berger and Selke imply). In fact the contrary view is put by Casella and R Berger
‘…the point null is more the mathematical convenience than the statistical method of choice. Few experimenters, of whom we are aware, want to conclude that “there is a difference”. Rather they are looking to conclude that “the new treatment is better”. ‘ (p106) See http://www.phil.vt.edu/dmayo/personal_website/casella%20and%20bergernocover.pdf
In fact Jeffreys was very proud of his significance test because it did something different. That something different was achieved by putting a lump of probability on the null hypothesis and he regarded this as a radical step.
d) I would maintain that having taken the radical Jeffreys step, the relevant probability for choosing to regard yourself as having obtained evidence in favour of H1 is no longer P(H0 <0.05) but P(H0<0.5) (where P here is a posterior probability). It is this, I think, that explains the fact that significance tests are often conservative when it comes to model selection.
e) My reading of the literature is that scientists rarely state the null hypothesis. In drug development there is a general agreement that we carry out one sided tests at the 2.5% level but describe them as 5% two-sided. This is covered in detail in Chapter 12 of Statistical Issues in Drug Development already provided to you.
f) I would say that since I don't confuse a P-value with a posterior probability I don't have the problem of deciding what the prior distribution on the null is. The P-values is simply what it is. If and when I need a Bayesian posterior probability I will calculate one.
g) Stating "the fact is" as a way of proving a fact is a rather weak defence,. Have you got anything else to offer?
Oh dear Stephen, if I were not so charitable, I’d be tempted to think you were being a tiny bit perverse.
I am not defending either. I’m mimicking what people actually do!
And I have never for a moment suggested that “P values are a mistake”. They do what they claim to do. What I have said is that what P values answer a question that is different from the one that experimenters want to ask. That’s quite different.
Keith: I have no direct access to a library so I have not yet
found an article by Mike Evans on posterior/prior being the more
relevant definition of evidence. I had a look at his web page but
none of the titles helped. I did however read his contribution to the
discussion of Deborah Mayo’s paper in Statistical Science. If the work
you mention is in the same vein then I will not be convinced by
it. The word `true’ is used without a hint of inverted commas: the
whole paper is in the `behave as if true’ mode. I refuse to work in
this mode. My degree of belief in any stochastic model is zero. We can
play games in this mode but I regard them as fruitless. I regard all
discussions about the likelihood principle as fruitless. One notes a
strong tendency to use substitutes for the word `true’ to dilute the
consequences. `Adequate’ is a popular choice, my memory tells me
that it was Birnbaum’s choice. But saying a model is adequate is
infinitely weaker than saying it is true. Two different models cannot
both be true but two different models can both be adequate. The Dutch
book argument fails and with it the whole of Bayesian statistics.
Lauriedavies2014:
I’m fairly sure I don’t know where this thread was intending to be going, but posterior/prior I thought was the typical “bayes boost” measure that follows from defining evidence as an increase in posterior.
The “adequacy” of models is of course the typical way of speaking, but are you happier with assigning degrees of belief to a model’s adequacy?
On Dutch books, the fact that it’s common for Bayesians to retract it nowadays , is why I list it as an example under “whatever happened to Bayesian foundations?” in a book I’m writing. Yet Bayesians, many of them, claim not to care that there’s no reason to apply Bayesian conditioning, no normative force for Bayes rule, and much else. Just one blog post that comes to mind:
You define adequacy in a precise manner, a computer programme., there are many examples in my book. The inputs are the data and the model, the output yes or no. You place your bets beforehand, run the programme and win or lose your bet. The bets are realizable. If you bet 50-50 on the N(0,1) being an adequate model, you will no doubt bet about 50-50 on the N(10^-20,1) also being an adequate model. Your bets are not expressible by a probability measure. The sum of the odds will generally be zero or infinity. If they have given up Dutch books have they also given up coherence?
Laurie: If you read my current post, you’ll see I describe we error statisticians as groping “our way and at most obtain statistically adequate representations of aspects of the data generating mechanism producing the relevant phenomenon.”
You ask “If they have given up Dutch books have they also given up coherence?”
Yes they mostly have, but not for this reason. (Please correct me Bayesians if I’m wrong.) The thing is,as many people have shown, avoiding Dutch books doesn’t require assigning probabilities to claims, nor that my bets be expressible by a probability measure. So that’s not why they accept incoherence. It’s because, or largely because, they want to use methods that violate the likelihood principle, either in attaining priors or checking models. Yes, the principle you regard as “fruitless” to discuss. Yet it is still presented as a theorem in dozens of texts, with the simple but incorrect “proof”. But back to coherence.
I’m disappointed that the reason many give for violating coherence is that our models are inexact. This lets them regard their incoherencies as minor “technical violations”. The presumption seems to be that Bayesian coherence would be achievable and desirable if only we had perfect knowledge; it’s an ideal. It becomes a kind of approximation error, whereas I think it goes much deeper.
Well, anyway, we’ve run together lots of very, very different topics in the discussion of this post.
Response to Corey
“You seem very confused as to what statisticians (frequentists and Bayesian alike) think you’re doing when you perform your simulations and generate your FDRs.”
I have very little interest in the internecine warfare between different tribes of statisticians. It gives rise to too much immoderate language, as the comments here illustrate.
My interest lies in the interpretation of experimental data. I don’t see how any practising scientist can take seriously subjective probabilities as any sort of quantitative measure. I (and many professional statisticians, sadly absent from the discussion) think that it is possible to put a rough minimum on the FDR without resorting to subjectivity.
I am still waiting for somebody to explain how it is that simulating what just about everyone does in real life gives an answer that’s wrong or misleading. Several people have been keen to tell me, rather bluntly, that there is a problem. Nobody has yet said what it is.
For example, some people have poured scorn on the point null. They may or may not be right to do so, but that isn’t the point. The fact is that the vast majority of people use it, and it’s the methods that people use which I was investigating
David:
It may be true that there is “internecine warfare between different tribes of statisticians” but surprisingly enough, your position has seemed to result in agreement among these very different tribes in questioning your interpretation and gambit. Readers of this blog have taken up that applet of J. Berger (2003) many times before (and even Jim said it was only to illustrate what would happen if we used one of his default .5 priors).
You want to view H’ as having been randomly selected from an urn of nulls where it is known that 50% are true, and regard this as giving Pr(Ho) = .5, but, as several of the commentators have pointed out, this is not a legit frequentist prior, and further, we wouldn’t know the % of true nulls, nor which urn to claim this one was randomly selected from.
In those very special, atypical, cases in which a prior prevalence is both available and relevant to evaluating the evidence for this particular H’, there is still grave doubts about the .5 prior. I have twice posted the comment: The spike .5 prior on the null is not innocent or impartial.
Casella and R. Berger (1987) show that “concentrating mass on the point null hypothesis is biasing the prior in favor of H0 as much as possible” (p. 111) whether in 1 or 2-sided tests.
You might want to look at the following post:
—————————————-
Here’s a new point. Let’s see if I got this right:
You start with .5 prior probability to the null.
You observed a statistically significant result with no bias, so it’s an actual .05 result.
You infer that the posterior probability of the null is .24, and claim this is actually evidence for no effect.
But you’d be wrong 76% of the time, right?
And of course, if you observed a non-statistically significant result, you’d also say there’s evidence of no effect, even much more so. Right? So your analysis had no chance of finding evidence of a real effect even if one exists. So it would fail on an actual error statistical analysis, which yours is not, any more than J. Berger’s is (e.g., that applet he published in 2003, a paper I commented on).
If someone said they had evidence of Ho: drug X is harmless, even though there was a statistically significant result in the direction of harm, and I discovered that person had no chance of finding evidence of the harmfulness of drug X, even if it was harmful, then I’d say
Ho: drug X is harmless
had passed a test with 0 severity.
Thanks very much for that response. We are beginning to get somewhere now.
I’ll take your second “new point” first.
I would never say that there is “evidence of no effect”. I would say rather that there is “no evidence of an effect”. That’s not quite the same thing and I have always thought of the former wording as being a statistical solecism. So it’s not right to say
What I actually said (in section 10) was
Of course it follows that 74% of positive tests are true positives. That’s well short of the 95% which many people imagine they are getting. But I can’t see why you say that “you’d be wrong 76% of the time” on the basis of these results.
Now to your first point. You said
I guess this is the trickiest bit and the discussion here has certainly made me think about it again. It’s certainly not as obvious as in the screening case.
How about the following argument?
(1) You know that some experiments you do will have a real effect, and others won’t. That’s self-evident and indubitable.
Of course it is right to say that any individual hypothesis is either right or wrong: in that sense it’s true that P(H) = 1 or 0. So you have to imagine a population of similar experiments in some of which there is a real effect and in some of which there isn’t. This is similar to what happens over ‘a lifetime of experiments, except in real life the chances that there is a real effect will vary from one sort of experiment to another. So you have to imagine that your experiment is a random sample from a hypothetical distribution of all possible repetitions of the experiment that you did, in which a certain proportion, P(H), of effects were real and others were not. The idea of a random sample from a hypothetical distribution of repetitions is a pretty standard manoeuvre in statistics.
(2) In any particular case, you have no real idea whether there will turn out to be a real effect or not. So let’s try various values of P(H). The example above was for P(H) = 0.5. That’s not chosen because of any thoughts about equipoise, but because it is the most favourable case, in the sense that if you use P =< 0.05, it gives a false positive rate (6%) that’s scarcely bigger than alpha.
(3) There is no point in considering P(H) values greater than 0.5. Not only would they imply astonishing prescience in your choice of experiment, but also if most experiments actually had real effects, then obviously most positive tests will be right.
(4) Research is risky and you’d be very lucky if half of your hypothesis turned out to be true. If only a tenth of them were true the false positive rate rises to 76% in the example above. This implies that the choice of P(H) = 0.5 provides, for practical purposes, a minimum false positive rate.
(5) It is the case that the minimum inferred from simulations is quite similar to that postulated by Sellke et al, using different arguments (29%) and by Valen Johnson’s uniformly most powerful Bayesian tests. This could be a coincidence, but I’d suggest that it isn’t, and that it supports my view that, in the sort of experiment under discussion, the false positive rate will usually be much higher than alpha.
We’ve already debated these points when I was under my DNS guise but let’s briefly mention it again. I think your point applies to many situations. But still regarding your point 3 I think you’re being overly pessimistic. The probability of many basic research hypotheses being true is arguably better than 50%. A lot of basic research is incremental and builds on previous findings.
I suppose the actual prior probability varies with the “surprise value” of some research. Following that logic you would expect to see a higher false discovery rate for high impact journals than specialised lower impact ones. I’m sure there are also a lot of additional factors. Certainly the quality of the underlying theory that generated the hypotheses plays a role too – my guess is that if I find evidence for telepathy it is likely to be a false positive.
Well if you just look at what get’s published, you might well think that the probability of guess ing the outcome correctly was over 0.5. But what gets published includes all the false positives and excludes all the unpublished negatives. If you can do experiments that conform your views more than half the time you must be a genius”
I am not talking about what gets published. I am sure this is skewed because publication bias is inherent to our system.
But if a hypothesis builds on established previous findings or is grounded in theory, it seems reasonably likely that a significance test will reject the null. It shouldn’t always just be a coin toss (or worse, as you suggest). But it’s an interesting question. As I said, you may be right as far as large parts of the literature are concerned.
Sam you say a hypothesis is likely to be true if “it’s grounded in theory”. I simply disagree. In biology, at least, there is very little theory that has real predictive ability. That’s true even in my field, which is almost closer to physics than biology. When it comes to the brain, most “theory” is little more than arm-waving.
Sorry but I just don’t buy that. I don’t know about your line of work but I can think of many situations where you should be likely to reject the null in neuroscience or psychology or biology. Take an effect that has been observed before, say the Stroop effect or photosynthesis or preferential fMRI responses to faces in the fusiform gyrus. Now your experiment tests some modulator of that effect, e.g. the conditions under which the Stroop effect occurs or whether face-sensitive responses are also observed for dog faces. You can’t honestly believe that for most such incremental research the odds of the predicted effect being real is 1/10.
I’d guess in many cases the more converging prior evidence your predictions are based on the higher the probability of it being real. If I predict that I can replicate the Stroop effect with some new fangly stimulus then that seems to me far more likely to succeed than predicting that I can send telepathic messages.
Anyway, you have a whole different discussion going on here… Wasn’t really trying to interrupt.
Well your intervention matters insofar as my objections would be much reduced if, say, 80 percent of the hypotheses that you test were actually true. I can’t disprove your assertion, and you can’t verify it. But it sounds desperately implausible to me.
We can formulate our problems in precise mathematical terms (based on physics. not empirical models) -e.g http://www.onemol.org.uk/?page_id=175 But we can’t yet begin to predict the effects of changing a single amino acid in channel protein.
I’m quite surprised that you use fMRI as an example, because that is an area that has been beset by horrendous statistical problems (remember the dead salmon fiasco). I guess that’s why some people refer to fMRI as the new phrenology!
To be honest I would be very interested in finding out how true that is. We can’t do it for new hypotheses obviously, but in the end it’s an empirical question. With the rise of preregistered experiments it should be possible to conduct a large scale meta-analysis of it. But perhaps it’s too unwieldy and impossible to get reliable estimates.
Regarding fMRI, don’t get me started on that phrenology nonsense. A friend of mine described this as “The dead salmon is a red herring”. My alter ego was planning to write a blog post entitled “Stop flogging a dead fish”. I might yet do this – but it’s definitely outside the scope of this discussion here so I’ll shut up. My postdoc made a nice demo though: https://twitter.com/sampendu/status/526842732913123328
David: No time now for more than one point: if you say the p-value is evidence of no or low effect (or even poor evidence of a real effect) whenever you get a p-value of .05, and you claim
Pr(null true|p-value of .05) = .24, Pr(effect is real|p-value of .05) = .76, then you’re wrong in dismissing it with prob .76.
I have discussions on these points in my book which I’m duty bound to finish in next couple of months.
I will later write the point I wanted to clarify with Senn on using tail areas a likelihood ratios.
By the way, you can’t just dichotomoize to the point null and an alternative against which a test has .8 power.
I’m sorry, but I just can’t follow that at all. What am I “dismissing with prob 0.76”? Nothing that I can see.
And as I have just explained , I don’t say “the p-value is evidence of no or low effect , , , whenever you get a p-value of .05”. On the contrary, I just described statements like that as solecisms.
I look forward to a full response when you get time.
David: The point is this: spoze we follow your recommendation of reporting either no or low evidence for a real effect upon getting a .05 p-value, then we will be asserting this wrongly with probability .74.
The type 2 error is high.
For a start, I didn’t say that P = 0.05 means “no or low evidence for a real effect””
I suggested, tentatively. that P = 0.05 might be described as “weak evidence: worth another look”.
See http://rsos.royalsocietypublishing.org/content/1/3/140216#comment-1889100957
That’s not so different from what the more sensible P value enthusiasts would say. It’s experimenters who make the mistake of claiming a discovery when they get P=0.04
Neither did I suggest that P values were worthless and shouldn’t be calculated. Quite the contrary.
Yes it’s obvious that it you want to be more sure there’s a real effect by demanding a lower P value, you’ll increase the risk of missing real effects. That’s discussed in my paper.
By all means criticise what I’ve said, but it’s unhelpful to criticise things that I haven’t said.
David: By thus weakening what you claim is warranted based on your .24 posterior, your argument that P-values fail to tell us what we need to know completely collapses. If all you’re saying is that an isolated .05 P-value gives no more than evidence for another look—which is the basis for Fisher’s insistence that we never report evidence of an effect from an isolated P-value–then there is no criticism whatsoever about P-values and no evidence what they tell us is not what we want to know, or any such thing. And this is granting your biased .5 to the point null.
On the other hand,if we take seriously that David C.’s finding a posterior prevalence of .24 for the null given a P-value of .05 is actually low evidence for an effect, , then (with probability .76) you erroneously fail to alert us even when there’s observed positive evidence of an increased risk.
So it turns out that at most you are complaining about people violating Fisher’s stipulation or misinterpreting p-values. I thought for a minute you were saying that what we really want to know in appraising the evidence for an inferred effect IS the posterior prevalence rate.
I’m sorry I have no time to read your paper, so let me just ask that you reread the comment I wrote to Byrd about the harms of evaluating the evidence from significance tests in the manner you recommend, i.e., looking for a posterior prevalence based on some intuitive guess about the % of “true effects” in the field.
May I suggest gently that if you are going to criticise a paper, there’s a good case for reading it first?
David: I never set out to criticize your paper; this was Senn’s post, and the discussion revolves solely around the post (which I don’t see as revolving around your screening paper). As it happens, I’m very familiar with this line of “argument from screening” (for at least 25 years) and have kept to the general points as raised in the post. That is the rule of this blog.
The issue first arose in a comedy hour on this blog:
I suspect particular problems which have to do with the likelihood ratio I’m guessing that you use, but until I look at the paper, I wouldn’t mention those.
Here’s a link to the Casella and R. Berger (1987) paper, if readers are interested:
Click to access casella-and-bergernocover1.pdf
[Blog Editor: due to Technical difficulties, I am entering COREY YANOFSKY’S latest comments for him.]
From Corey Yanofsky:
In reply to https://errorstatistics.com/2015/03/16/stephen-senn-the-pathetic-p-value-guest-post/comment-page-1/#comment-119722:
Lauriedavies2014: I wonder if you ever actually ran this argument past even one Bayesian to see what they would say. Here, let me.
As you say, if I bet 50-50 on the N(0,1) being an adequate model, I will no doubt bet about 50-50 on the N(10^-20,1) also being an adequate model, and my bets are not expressible by a probability measure in a probability triple where some set of statistical models (call it M) is the sample space. But that doesn’t mean they’re inexpressible by any probability measure whatsoever! In this setup the appropriate sample space for a probability triple is the powerset of M, because exactly one of the members of the powerset of M is realized when the data are observed.
For example, suppose that M = {N(0,1), N(10^-20, 1), N(5,1)}; then the appropriate sample space is isomorphic to the numbers from 0 to 7, with each digit of the binary expansion of the integer interpreted as an indicator variable for the statistical adequacy of one of the models in M. Let the leftmost bit refer to N(0,1), the center bit refer to N(10^-20, 1), and the rightmost bit refer to N(5,1). Here’s a probability measure that serves as a counterexample to your claim: Pr(001) = Pr(110) = 0.5, Pr(000) = Pr(100) = Pr(101) = Pr(011) = Pr(010) = Pr(000) = 0.
Now obviously when M is uncountably infinite it’s not so easy to write down probability measures on sigma-algebras of the powerset of M. Still, that scenario is not particularly difficult for a Bayesian to handle: if the statistical adequacy function is measurable, a prior predictive probability measure automatically induces a pushforward probability measure on any sigma-algebra of the powerset of M.
[Blog Editor: due to technical difficulties, I am entering COREY YANOFSKY’S comment for him.]
From Corey Yanofsky:
In reply to https://errorstatistics.com/2015/03/16/stephen-senn-the-pathetic-p-value-guest-post/comment-page-1/#comment-119744:
David: Mayo put her finger on the key point I was trying to convey — for all of our differences, I believe the two schools of statisticians would agree that you’ve failed to understand why frequentists might look askance at simulations with an assumed prevalence of false nulls. I can illustrate why by critiquing this claim: “I… think that it is possible to put a rough minimum on the FDR without resorting to subjectivity.”
The minimum FDR for p = 0.047 occurs when the prevalence of false nulls is 0%, not 50%. (Then the FDR is also 0%, obviously.) The choice of 50% as the prevalence of false nulls (as opposed to, say, 40% or 60%, or 1% or 99% for that matter) isn’t backed by any data that I’m aware of. Correct me if I’m wrong, but it’s just the minimum value you consider plausible. This puts the analysis firmly in the subjective Bayesian style, albeit you don’t seem to know enough about the internecine (and admittedly tiresome to outsiders who lack the fire of righteousness in their bellies) squabbling of the two schools of thought to recognize this. The problem (or at least, a problem) frequentists have with the 26% FDR you’ve simulated is that it is exactly as well-grounded as that 50% prevalence.
(Those specifically in Mayo’s “error-statistical” school have different, more foundational objections, but it would be superfluous for me to try to do them justice here.)
Corey Yanofsky.
You are right when you surmise that P(H) = 0.5 is “just the minimum value you consider plausible”
It’s self-evident that if most of the hypotheses you test are correct, then you won’t have many false positives,
But you surely don’t expect anybody to accept a system of inference that’s based on the assumption that you guess correctly most of the time. If you were to submit a paper that said the statistics show that I’m right based on the assumption that I’m usually right, you’d have the reviewers rolling on the floor laughing, and quite rightly so.
I fear that your suggestion shows that your theoretical considerations have last all contact with experimental realities.
David, I find your reply baffling — I haven’t made any suggestions or stated any theoretical considerations in my comments to you. You’re being a little too quick to ascribe ridiculous positions to me; slow down there…
Well I read your comment as a criticism of my statement that 26% was the minimum FDR (for tests of the sort that I simulated). That criticism is quite right, if you allow P(H) > 0.5.
I was merely pointing out that P> 0.5 would be utterly unacceptable to experimenters and to reviewers. So I should have said that, for any P(H) that would be considered acceptable, the minimum FDR is 26% Do you agree with that version?
First of all, I am not sure I agree with assigning probabilities to hypotheses (the whole random variable debate..).
Second, I am not sure how you can say with such assurance that “P(H)>0.5” (if such a thing did exist) is not acceptable to experimenters/reviewers. Part of our job is (a) making sure that we are really sure of what we think we are sure of, (b) asking whether we are justified in what we are sure of. Both of these cases assume a “P(H)>0.5”. (a) refers of course to replication/triangulation, (b) refers to breaking down pre-existing myths or questioning pre-existing “knowledge”.
By saying that “P(H)>0.5” is not interesting, I think your position is not that different at some level from “let’s pay attention to only p-values<0.05” – clearly a plague we need to rid the world and reviewers of. The problem with both approaches (the above and yours) is that they prize novelty; but define novelty as something we didn’t know or were not sure of before.
The more appropriate view of “novelty” is of course the tautological “something new” – this could be:
i) showing something we previously strongly believed in (but not completely) to have some specific problems.
ii) showing something we previous strongly believed in to have more evidence.
iii) showing something we previously didn’t believe in to have some supporting evidence.
iv) showing something we previously didn’t really believe in to be unsupported.
To me all of them (i-iv) are scientifically interesting and should be pursued. It should be obvious that the prior of a hypothesis [P(H)0.5] by itself is a little bit besides the point. There is no clear way in which P(H) < 0.5 are the only interesting cases – modulo how the reviewing process works.
Karthik
” I am not sure how you can say with such assurance that “P(H)>0.5” (if such a thing did exist) is not acceptable to experimenters/reviewers.”
As I already said, to assume in advance (with no objective justification) that the experiment was almost sure to succeed (P(H) > 0.5), and then to conclude that it succeeded would be very close to tautology. Any sensible person would laugh at such a suggestion.
Of course there is nothing magical about 0.5 apart from its suggestion of equipoise. In real life, it would be a huge achievement if as many as half your hypotheses turned out to be true. It’s well known to anyone who does experiments that most bright ideas fail when put to the test. It’s one of the problems that the failures often aren’t published so the literature gives a hubristic impression of science.
We are now paying the price of that hubris, insofar as science is getting s reputation for irreproducibility. Surely it is part of the job of statisticians to help with that problem. Some of the comments here strike me as a hindrance rather than a help.
David: Wasn’t planning to write, but now you sound like Berger and Sellke who invent a .5 prior in the null so that their rejections look impressive.:
[I]t will rarely be justifiable to choose [the prior for the null] π0 < 1/2; who, after all, would be convinced by the statement ‘I conducted a Bayesian test of H0, assigning prior probability .1 to H0, and my conclusion is that H0 has posterior probability .05 and should be rejected’? (Berger and Sellke, 115)
But at least they admit to being Bayesian. You're imagining that your evidence for this particular H' would be either laughed at or taken seriously all depending on some imagined % of the prevalence of true nulls in the urn of nulls from which yours was taken? Maybe your inference to H' is a representative of experiments that you work 4 years showing you've got a genuine effect, stringently ruling out mistakes. Why should THAT information hurt rather than help the weight given to your current inference? David has a stellar record, and this inference is bound to be well warranted too!
@David: You are just repeating yourself. I gave you a list of 4 different things that scientists are and should be interested (although, the current review process kills some of them).
Are you specifically saying that not all of the i-iv I listed are not important or even acceptable?
You are effectively stating by diktat that this is the case instead of providing an argument. I too am familiar with other scientists being one myself, and so it is not obvious to me at all when you say “scientists care about…”, because I am aware of many scientists who don’t only care about the issue you mentioned, but also the others I mentioned in the list of i-iv.
So, your speaking on behalf of all scientists or “sensible”scientists ironically seems to be hubristic in itself.
So, if you have an argument for why P(H) < 0.5 are the only interesting cases, when as I see it all i-iv are interesting, then please make that argument. But, repeating yourself while ignoring what I have said is not productive.
David, it is a criticism — it’s just not a criticism I’m actually making. I’m attempting to communicate what I think a doctrinaire frequentist would say about it. Recall that the position I’m defending is that you’re confused about how Bayesians and frequentists alike view your simulation studies: to wit, as essentially Bayesian.
I’d like to really highlight that the kind of plausible reasoning you’re trying to do here is Bayesian in nature — not just because Bayes’s Theorem is used to calculate the FDRs but because you’re attempting to figure out what is reasonable to believe given the information available to you. I personally agree that P(true null) = 0.5 and power = 0.8 are exceedingly generous numbers and 26% is a loose lower bound for the discipline-wise FDR in many fields. Heck, I think that .the assumption that p-values are uniform under the null is generous, for reasons given here: http://andrewgelman.com/2013/09/26/difficulties-in-making-inferences-about-scientific-truth-from-distributions-of-published-p-values/.”
Mayo, you’re probably going to have to send David a copy of EGEK before he’ll begin to understand why you think prevalences are not relevant ;-). The power = 0.8 value is probably a more generous assumption than most studies deserve, so it’s a reasonable value to use for computing a lower bound.
David/Corey: The real problem, aside from the fact that these prior prevalences aren’t known and aren’t relevant if known, is that the null is given .5 as is the alternative against which the test has high, say, .8 power, call it H'(.8). These two don’t exhaust the parameter space. The denial of H'(.8) is not the null. I directed David to the relevant post on this quite a long time ago.
I agree that prior prevalences are not relevant to P values. But since P values don’t answer the question that experimenters want to ask, one has to try to answer the right question. I simply can’t agree that prior prevalences are irrelevant to that question. One only has to look at what happens with very low, or very high, prevalences to see that..
“From the table, the probability is 0.9985, or the odds are about 666 to one that 2 is the better soporific.” (Student, 1908)
Student is making that pesky error. You CANNOT conclude it is a “better soporific” just by seeing that one average is higher than the other. That is disproving strawman hypothesis A in order to conclude substantive hypothesis B. You can only say “the data in column 1 was higher on average than the data in column 2”.
First, in Student’s table treatment “1” refers to the Dextro- isomer of hyoscyamine hydrobromide, while “2” refers to the Levo- isomer. If we find the paper where the data originated (Cushny and Peebles, 1905) we find that Student has mis-transcribed the table. The data he compares is actually Levo-Hycosamine to Levo-Hycosine (i.e. Scopolamine). So the conclusion he forms is wrong due to the most mundane of experimental artifacts.
Ignoring that, Cushny and Peebles (1905) contains essentially no methodological information. How was sleep measured? How was initiation of sleep determined, what about termination? How did they deal with patients who awoke transiently in the middle of the night? How did they distinguish between “sleeping” and just laying there quietly?
Perhaps the treatment made the patients more or less anxious/agitated. If they were more anxious they may tend to fake sleep to avoid interaction with the staff or each other, if less so they may be simply less motivated to get up and do things. Perhaps the treatment caused constipation or urinary retention. How common are midnight trips to the bathroom in those wards?
How were the compounds stored? Are we sure that hycosamine isn’t just less stable than hycosine under those conditions? Shouldn’t determination of which is “better” also include some assessment of cost of purchase, storage, and side effects?
Student also only looks at “additional hours of sleep” rather than the raw values. If we inspect the latter some questions of plausibility arise. Is it really plausible that patient #1 slept ~1.5 hrs a night for an entire month?
Cushny and Peebles (1905) write: “As a general rule a tablet was given on each alternate evening, and the duration of sleep and other features noted and compared with those of the intervening control night on which no hypnotic was given.” It sounds like they did not assess the amount of day-time sleep at all. It is plausible that the treatment reduced sleep the first night, leading to more daytime sleep the next day, followed by lower than normal sleep during the control night, making them more tired the next night, etc. The data is not reported in enough detail to say.
I do not think the people recommending these significance tests to scientists really understand the paucity of information they provide. That is why so many researcher’s end up confused, they refuse to accept that they have to spend time learning something that offers them so little so they make up myths about what it can accomplish.
Student, The probable error of a mean. Biometrika, 1908. 6: p. 1-25.
The action of optical isomers II. Hyoscines. Arthur R. Cushny and A. Roy Peebles.Journal of Physiology v.32(5-6); 1905 Jul 13
http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1465734/
Pingback: eruditely comments on “P values are not as reliable as many scientists assume (2014)” | Exploding Ads