Stephen Senn
Head, Methodology and Statistics Group
Competence Center for Methodology and Statistics (CCMS)
Luxembourg
Responder despondency: myths of personalized medicine
The road to drug development destruction is paved with good intentions. The 2013 FDA report, Paving the Way for Personalized Medicine has an encouraging and enthusiastic foreword from Commissioner Hamburg and plenty of extremely interesting examples stretching back decades. Given what the report shows can be achieved on occasion, given the enthusiasm of the FDA and its commissioner, given the amazing progress in genetics emerging from the labs, a golden future of personalized medicine surely awaits us. It would be churlish to spoil the party by sounding a note of caution but I have never shirked being churlish and that is exactly what I am going to do.
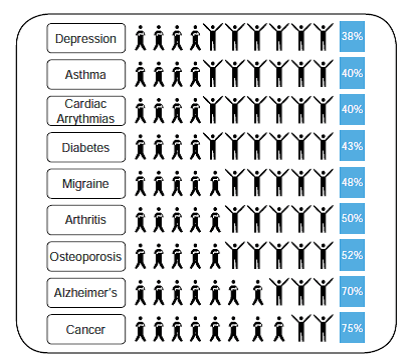
Reading the report, alarm bells began to ring when I came across this chart (p17) describing the percentage of patients for whom drug are ineffective. Actually, I tell a lie. The alarm bells were ringing as soon as I saw the title but by the time I saw this chart, the cacophony was deafening.
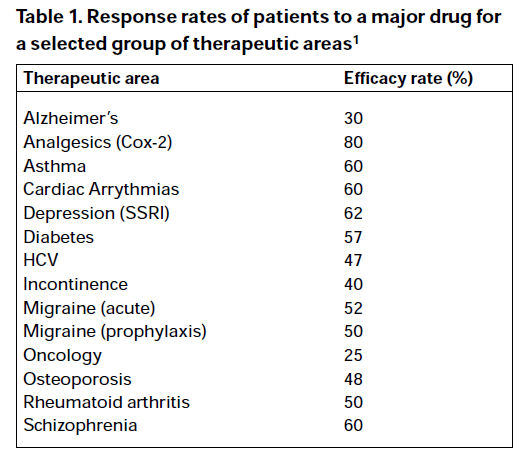
The question that immediately arose in my mind was ‘how do the FDA know this is true?’ Well, the Agency very helpfully tells you how they know this is true. They cite a publication, ‘Clinical application of pharmacogenetics’[1] as the source of the chart. Slightly surprisingly, the date of the publication predates the FDA report by 12 years (this is pre-history in pharmacogenetic terms) however, sure enough, if you look up the cited paper you will find that the authors (Spear et al) state ‘We have analyzed the efficacy of major drugs in several important diseases based on published data, and the summary of the information is given in Table 1.’ This is Table 1:
Now, there are a few differences here to the FDA report but we have to give the Agency some credit. First of all they have decided to concentrate on those who don’t respond, so they have subtracted the response rates from 100. Second, they have obviously learned an important data presentation lesson: sorting by the alphabet is often inferior to sorting by importance. Unfortunately, they have ignored an important lesson that texts on graphical excellence impart: don’t clutter your presentation with chart junk[2]. However, in the words of Meatloaf, ‘Two out of three ain’t bad,’ so I have to give them some credit.
However, that’s not quite the end of the story. Note the superscripted 1 in the rubric of the source for the FDA claim. That’s rather important. This gives you the source of the information, which is the Physician’s Desk Reference, 54th edition, 2000.
At this point of tracing back, I discovered what I knew already. What the FDA is quoting are zombie statistics. This is not to impugn the work of Spear et al. The paper makes interesting points. (I can’t even blame them for not citing one of my favourite papers[3], since it appeared in the same year.) They may well have worked diligently to collect the data they did but the trail runs cold here. The methodology is not given and the results can’t be checked. It may be true, it may be false but nobody, and that includes the FDA and its commissioner, knows.
But there is a further problem. There is a very obvious trap in using observed response rates to judge what percentage of patient respond (or don’t). That is that all such measures are subject to within-patient variability. To take a field I have worked in, asthma, if you take (as the FDA has on occasion) 15% increase in Forced Expiratory Volume in one second (FEV1) above baseline as indicating a response. You will classify someone with a 14% value as a non-responder and someone with a 16 % value as a responder but measure them again and they could easily change places (see chapter 8 of Statistical Issues in Drug Development[4]) . For a bronchodilator I worked on, mean bronchodilation at 12 hours was about 18% so you simply needed to base your measurement of effect on a number of replicates if you wanted to increase the proportion of responders.
There is a very obvious trap (or at least it ought to be obvious to all statisticians) in naively using reported response rates as an indicator of variation in true response[5]. This can be illustrated using the graph below. On the left hand side you see an ideal counterfactual experiment. Every patient can be treated under identical conditions with both treatments. In this thought experiment the difference that the treatment makes to each patient is constant. However, life does not afford us this possibility. If what we choose to do is run a parallel group trial we will have to randomly give the patient either placebo or the active treatment. The right hand panel shows us what we will see and is obtained by randomly erasing one of the two points for each patient on the left hand panel. It is now impossible to judge individual response: all that we can judge is the average.
Of course, I fixed things in the example so that response was constant and it clearly might not be. But that is not the point. The point is that the diagram shows that by naively using raw outcomes we will overestimate the personal element of response. In fact, only repeated cross-over trial can reliable tease out individual response from other components of variation and in many indications these are not possible and even where they are possible they are rarely run[6].
So to sum up, the reason the FDA ‘knows’ that 40% of asthmatic patients don’t respond to treatment is because a paper from 2001, with unspecified methodology, most probably failing to account for within patient variability, reports that the authors found this to be the case by studying the Physician’s Desk Reference.
This is nothing short of a scandal. I don’t blame the FDA. I blame me and my fellow statisticians. Why and how are we allowing our life scientist colleagues to get away with this nonsense? They genuinely believe it. We ought to know better.
References
- Spear, B.B., M. Heath-Chiozzi, and J. Huff, Clinical application of pharmacogenetics. Trends in Molecular Medicine, 2001. 7(5): p. 201-204.
- Tufte, E.R., The Visual Display of Quantitative Information. 1983, Cheshire Connecticut: Graphics Press.
- Senn, S.J., Individual Therapy: New Dawn or False Dawn. Drug Information Journal, 2001. 35(4): p. 1479-1494.
- Senn, S.J., Statistical Issues in Drug Development. 2007, Hoboken: Wiley. 498.
- Senn, S., Individual response to treatment: is it a valid assumption? BMJ, 2004. 329(7472): p. 966-8.
- Senn, S.J., Three things every medical writer should know about statistics. The Write Stuff, 2009. 18(3): p. 159-162.







I’ve seen a lot of misleading charts, but that one makes me particularly uncomfortable. The “respondent” stick figures, with their arms raised in joy, occupy more space than non-respondent figures do (on an individual basis, they’re about ~1.8x as wide!), suggesting that the proportion of successful cases is larger than the listed percentage. The non-respondent stick figures, with their arms crossed, are so understated in comparison…
I agree. It deserves some sort of a prize for an awful chart. Quite apart from the issue of accuracy I don’t see what the stick humans added apart from confusion.
Excellent, excellent post! I’ve been thinking about similar things for quite a long time. And, if I can offer one quibble, I really think that you expect too much of statisticians, at least the modern, predictive-modeling type, to expect them to call the FDA on things like this. In my opinion, this all stems from the reporting of, reliance on, and vast over-interpretation of point estimates. (I’m assuming here that the Physicians Desk Reference accurately reported values that they obtained from reported trials.) At one time, statisticians seemed to really understand what the sampling distribution was… and, thus, they understood that a point estimate is nothing more than a single random draw from an underlying distribution of unknown variability. The point estimate is in no way a “best estimate” (there is no such thing in statistical theory), it carries almost no statistical information. Yet, people do like certainty.
Thanks so much Stephen for this post. I too am skeptical of the “personalized medicine” hype (and that’s w/o all the insider info you have), especially after the Anil Potti case (which they don’t mention, unless I missed it).
Instead of the exuberance for some of the personalized clinical trials based on someone’s new big data model for cancer trials, the public should ask FDA what it can be doing instead of what it is doing (e.g.,to gain better substantive understanding of cancer, immunology,etc.). I’m not impressed with the carnival game of which poison to administer in these “adaptive” trials. After reading the “omics report” (linked to above), I began to think that there was a need for private medical-statistical experts to inform people about the nature of the trials, models, even philosophies of statistics behind a drug or trial they might be considering (I’d hire Stephen Senn’s group—if there were such a thing, and I needed the service.) Few medical doctors know more beyond the official reports and can’t critically appraise the latest info, particularly the statistics. In this day of wedding planners, and counselors for writing college applications, the time may have come for specialists in real “personalized” medicine. The public would become informed, rather than passive recipients of whatever those in power decide is best for us.
And while I’m kvetching, why don’t they do something to develop new antibiotics? Info from part of my other life (in biotech stocks, which I mostly stay far away from) makes it clear how much is determined by idiosyncratic trends in profits, regulations and patents. It’s well known that more and more bacteria are impervious to existing antibiotics, but it’s not profitable enough for companies to develop new ones. Why not change the patent laws for them so that we don’t keep heading toward the day where currently trivial infections are killers?
Mayo: Recently Scott Alexander of Slate Star Codex wrote a post that covered the question of antibiotic discovery rates. There are three main reasons why antibiotic discoveries have slowed. First, the economics: antibacterials are short-course drugs, and drug companies can make more money with drugs for chronic conditions. Second, regulatory: the FDA approves antibacterials based on disease state one at a time rather than based on the organisms the antibiotic is designed to kill, so getting an antibacterial to market only gets you a slice of the whole pie. Combined, these factors give investment in a new antibacterial a negative net present value. Third, the low hanging fruit have been picked. Most antibacterials come from soil bacteria, and we’ve used that platform up.
References for the above are an APUA Newsletter article and a Nature Reviews Drug Discovery review article.
Corey: Thanks so much for the links to other recent antibiotic discussions. So your points support my claim about lack of financial incentives. I don’t know about it being too hard to find new ones.
I’d never heard of this Slate Star blogger (not that I know many bloggers). I see hints that he might be part of one of the cosmic singularity cults–maybe not. (I think the problem with antibiotics is far more likely to be worrisome than an attack by unfriendly robots. We’re back to one of I.J.Good’s jokey speculations.) I’ll check the other links.
Corey: The APUA article is good. Your last link doesn’t work.
Mayo: Whoops! Try this.
Scott Alexander is a well-respected author at LessWrong; he hasn’t attended any CFAR workshops that I know of. Not sure if this qualifies him as a “cosmic singularity cult” member or not in your eyes.
Couple of points: 1. Actual cults require members to cut off contact with non-members so as to isolate them from other support networks; 2. LessWrong folk don’t predict a “rapture of the nerd” type singularity; we tend to think most artificial general intelligences that might be developed would not automatically be beneficial, and that it will take a significant amount of extra effort to create one that is. As a result, our preference is that more resources go to researching AI safety than researching improved AI performance.
Corey: Mainly just pulling your chain (on Sat night.) Nothing is “automatically beneficial”, and for that matter, the extra effort to make machines like us could backfire. (Do you read Stephen King?)
Mayo: I’ve read Stephen King in the past, but not for a long while. Does the phrase “make machines like us” mean “make machines have a liking for us” or “make machines similar to us”?
Corey: the former, I should have said, make them “friendly” or whatever term you use these days.
Mayo: The notion is less “machines that like us” and more like high assurance techniques for autonomous self-improving AI.
Corey: Are these techniques for high assurance that autonomous self-improving AI robots will promote human welfare and not destroy us? What are these techniques?
I’m not one of the people who worry about this, I’m addressing the goals of the large movement consisting of people who do (“singularity” people).
(I do worry about flash crashes, already happening, that we can’t understand.)
Mayo: The field’s in its infancy, so no one really knows. The work I’m aware of is aimed at getting around the logical difficulty that the proofs of a logical theory’s consistency can be made only in a stronger meta-, which would tend to suggest that an agent cannot reliably prove that a self-modification (or equivalently, replacement with a successor agent) will preserve desirable properties of the agent. (One approach being explored is to extend probability theory so that it can cope with logical uncertainty. This basically combines measure theory with model theory in ways that are beyond my ken.)
Corey: Strikes me as absurd, as if the problem is one of a “logical theory” and its “consistency”. What are the axioms? They can’t be set. What’s to be “preserved”? And reliably proving is oxymoronic.
As I say,we already have out-of-control results with financial robots: they interact with contingent facts of the world. We need more self-correction.
Mayo: I was going to write “meta-theory” but I was unsure of the correct jargon…
Mayo: There’s only been one flash crash, and it was followed by a flash recovery, so I’m pretty optimistic that this is not going to be a huge problem. A buddy of mine studying market microstructure at the Bank of Canada reports that the marginal value of entering a market as an HFT trader is approaching 0, so it seems that market saturation and competition are doing what they generally do…
Robot simulcra may be going out of style – but that hasn’t stopped companies from designing entities like the “childlike” Pepper, to haunt our nightmares:
http://www.cnn.com/2014/06/06/tech/innovation/pepper-robot-emotions/
Sleepy: I expect relationships with “operating systems” akin to the movie “her” will be common in the not too distant future. Too bad it was such a boring movie (even for a plane).
Mark: “I really think that you expect too much of statisticians, at least the modern, predictive-modeling type, ….At one time, statisticians seemed to really understand what the sampling distribution was…”
This captures my worst fears about the modern, predictive-modeling type.
@stephen thanks for your always-enlightening perspective. I always find that pharmacogenomics/pharmacogenetics is particularly enriched in bad statistics.
I think this is partly because biology does not have a strong tradition of dealing with observational data. People criticize epidemiology and economics for being pseudo-science, but at least they’ve been embarrassed enough times to take counterfactual thinking seriously.
Thanks. What is alarming is how much money has been sunk into this in drug development. There have been a few interesting successes and the main interest in the FDA paper is the examples of this that it brings. However, a proper audit of what has been spent and what has been achieved is lacking.
In general the whole issue of personalising medicine (what’s possible, what’s desirable, what’s economically practical) is very badly dealt with. the medical press doesn’t help. (See circus currently surrounding dabigatran as en example http://www.bmj.com/content/349/bmj.g4756)
Some day I must write about the phenotypic squeeze : how pharmacogentics is sandwiched between one size fits all and dosing on phenotype.
Yes that is a informative post. There are many other issues in the personalised medicine field. Take for example (dichotomous) biomarkers published based on statistically significant hazard ratios. No mention of calibration (maybe discrimination) nor the additional information above and beyond cheaper to obtain variables. Another source of variation is measurement error. If the ‘validation’ were run again even in the same laboratory would the same conclusion be made? It seems money can be made as the regulations so lax. Are these tests really helping anyone?
Article addition: Senn’s “Individual Therapy: New Dawn or False Dawn” can be accessed here.
I believe we do know better, though I recognize that there are some self-identified statisticians who can get things very wrong (witness the Duke Genomics fiasco).
I think the issue is numbers – there are so many more of them than us, and their culture includes derision of pedantic statisticians. How are the sensible among us to do battle with so many of them? It is not an easy pursuit, but we are making efforts. For example, the editor of the journal Science just announced the formation of a statistical board of editors to attempt to better assess the quality of statistical reasoning presented in submitted articles.
In my undergraduate and graduate studies, I observed that most people from non-statistical programs who took statistics classes really did not like them, whereas my fellow statistical colleagues loved the classes. I did not see many people at all who just kind-of liked statistics – it appears to be a love/hate relationship. Thus statisticians will always be in short supply, and we will always be noting some area or other where lack of sensible data and analysis leads people to say the silliest things based on fallacious evidence.
Referring back to the journal Science, I have lost track of how many life sciences papers I have skipped over after seeing error bars on a barplot column that extends up to 1.0 and denotes the normalized value for a control condition. Such graphics immediately indicate that the paper authors do not understand statistics appropriately, and engaged no statistician of worth in producing the analysis upon which they base their conclusions. No wonder John Ioannidis was able to produce a paper on why most published research is false.
The explosion of the biomedical field in the past two decades was not matched by an explosion in recruitment of statisticians into that field, as witnessed by the poor statistical handling of data in so many life sciences papers of this period. While it has been easy to recruit young undergraduates and graduates into life sciences, it has not, as always, been easy to recruit more statisticians into statistics programs, since so many people dislike statistics.
Professors in life sciences departments and life science researchers need to be regularly encouraged to include statistician time in their funding and grant applications, and to seek guidance from statisticians before rushing to publish. I happen to be fortunate to work for such a life scientist, but I see my situation as the exception, as few other life scientists in my geographical area have hired a statistician. Salaries in corporate jobs tend to be much higher than salaries in research jobs, so most statisticians are hoovered up into the corporate realm, where few are able to perform reasonable statistical oversight.
Thus to address this issue, top tier statisticians need to advocate heavily to organizations such as the US FDA, NCI, NIH , UK NHS etc. that grant applications must include funding for statistical support, government agencies must include statistical oversight for reports containing statistical materials, and journals must have a statistical board of editors as Science has recently set up. There’s so much evidence available now to support such arguments – so while I may not yet be ready to wag a finger at all my fellow statisticians at this point, I certainly agree that it is our responsibility to point out these problems in an appropriate tone, and advocate for better statistical support. Certainly your writings are valuable contributions towards this effort.
Hi Steven: When you say “no wonder Ioannidis…” you could mean, no wonder it’s true that most published statistical research is False , or no wonder star quality was given to his (non-empirical 2005) report based on assuming publishing at the first Stat Sig result with dichotomous testing, using size and power as a “likelihood ratio” for a “science-wise error rate” screening report–assuming high prior probabilities to the falsity of claims. I take it you mean the former, but there’s an argument for the latter. It was analytic he’d get the result he did, given the assumptions to dichotomous hypotheses:Either it’s true or false, no magnitudes. It may hold for given fields/practices but the blanket result has done more than anything else to confuse screening with an evidential appraisal of a given hypothesis, and everyone is now getting on the bandwagon (especially those who are only too happy to scapegoat significance tests for certain cases of irresponsible or bad science.) A serious distortion about high power tests, if followed, would advocate tests that pick up trivial discrepancies, rather than replicable ones. I could go on.
I
Mayo: All the evidence I see points towards Ioannidis’s title “Why most published research findings are false”. I have seen no evidence in the intervening 9 years to refute this claim. Recent attempts to replicate previous findings have only illustrated how correct this statement is. I think that PLoS Medicine paper has the star quality it has because so many people recognize the validity of the claim and the sensible arguments that comprise the paper. I certainly recognized that the analytics therein were reasonably stated and given what I know about the random nature of data and the current state of publish or perish academics and associated grant funding, the conclusions were immediately obvious. I’d rather say that Ioannidis describes a useful model that well illustrates why things are the way they are. The result is as far as I can see plainly empirical rather than analytic. I think Ioannidis had all the empirical evidence he needed to phrase the title of the paper (the first nine references provide ample support) – what he then needed was a useful model to describe the patterns observed, which the paper sets out. Simple basic statistical mathematics that beautifully show how incorrect conclusions result when inconvenient data and analytical findings are swept under the rug.
I have to deal with the issues described in that paper on a regular basis. In assessing yet another potential biomarker that appears to me to show little if any association with anything, I review the literature, and typically find four or five papers claiming this biomarker shows that the gene involved is a cancer causing gene, and another four or five papers claiming that the gene has a protective effect – in other words on average there is no there there. This is not helpful in the publish or perish environment, but I will not shade an analysis to allow a publication of some dubious positive component finding when all indicators suggest an overall null finding, no matter how much the other lab members grumble. How I wish null findings could be published honestly, as such. That would immediately allow for a large reduction in the rate of false claims, as people could honestly describe things that did not work so that others could avoid interpreting their false positive findings as “real”. I work in a cash-strapped largely government-funded environment, that tends to yield decisions to run many small experiments (though I regularly advocate against this practice) the results of which are directly reflected by all of the Corollaries that Ioannidis lays out.
Ioannidis proposes many sensible strategies to help curb this problematic state of affairs: better interpretation of the scientific significance of statistically significant findings (he even cites Stephen Senn on this! Ref 34), fewer studies with larger sample sizes, less competition and better appraisal of the likely value of the totality of evidence in given fields so that investigations into null relationships can be terminated sooner and other areas investigated.
While I agree with Stephen Senn’s sentiment that we as statisticians should not allow our life scientist colleagues to get away with the issues that create the environment that Ioannidis characterises in his paper, or Senn describes above regarding the silly FDA report, I’m not ready to blame Stephen Senn. He does know better and has clearly made efforts to guide colleagues away from such nonsense (he even describes such incidents in Ref. 34 of Ioannidis’s paper) which is why I look to his writings to help me in my efforts to dissuade. Those of us who know better need to keep up the effort – difficult as it is, it’s the only honest scientific approach.
Steven: I think you are referring to the totally right-headed criticisms Ioannidis raises under the heading of “bias” (failing to adjust for multiple tests, cherry picking,post-data subgroups, and the like) as well as some of the remedies recommended therein. I agree with those. I will respond further when I can.
@steven
As someone from a non-stats program who took a fair amount of stats I can agree with your general love/hate dichotomy (while at the same time I was a just-kind-of-like-it person, or had at least had a personal love/hate internal battle). With this in mind I think the reason is not just pedantry/rigour vs non pedantry/carelessness (which plays a part) but a more general difference in approach. This might not be applicable to the life sciences you focus on but I think could explain some of the stats/non-stats divide.
[@mayo – please excuse yet another excessively long comment from me. @stephen – really nice post, thanks]
In engineering/applied math/physics courses we spent almost all our time deriving mechanistic models based on physical principles; then we analysed the qualitative properties of possible solutions and if possible solved the models analytically. We probably spent too much time on methods for finding exact solutions but also spent a lot of time learning how to solve equations numerically eg finite difference/element methods and through approximate methods like perturbation series. We generally felt like we understood the models and their properties; we didn’t spend nearly enough time comparing these models to real data.
In our stats courses we spent a lot of time doing things like testing for differences in means between groups and fitting linear regression models without regard for mechanism. We had it drummed in that correlation is not causation (ie don’t use the word ’causes’), what a p-value was, all the steps for testing various assumptions and checking residuals and a template for writing a report on our findings. Everything was parametric and linear. We used R a lot which was nice but at a much simpler level than any of our other programming/numerical methods courses. The stats courses for doing statistical simulations were considered advanced topics so weren’t covered in the first couple of years, while we had our own courses covering that sort of thing anyway.
While I enjoyed the stats courses as something distinct from what we did in math/physics/engineering I think I and many others felt frustration that we weren’t learning things in a way that felt naturally complementary to our other courses. There was never much/any ‘ok you’ve got your differential equation model now let’s look at how to use stats to relate it to real data’. Any of that came through the non-stats courses. Even ‘advanced statistical modelling’ was doing multiple linear regression to death. Now that’s fine – stats is its own thing – but when computer scientists, engineers etc start reinventing wheels but using different language and applications a lot of people like myself secretly, and not so secretly, think ‘well at least now they speak the same language and are interested in similar things’. I’m not sure if this is a justified view but I think it’s relatively representative. I’ve certainly heard it anecdotally over and over.
My compromise has been to try to find physicists, engineers, computer scientists, ecologists (and philosophers!) etc turned statisticians who can translate the concepts. That’s not to say there aren’t great statisticians to learn from but it is often easier to learn starting from applications you’re familiar with. I’ve come to appreciate statistics a lot more through this; however I know some who do work relating models and data but still essentially hate stats! [Another reason for Bayes’ popularity – it’s ‘something different’, has a straightforward mathematical statement and usually involves simulation. Quantitative modelling folk find it hard to resist!]
Now I’m not sure if any of this is relevant for the life science ‘issues’ – they have their own culture as I’ve learned – but I think is relevant for the rise of ‘data science’ and all that, whatever that is.
omaclaran: So how do you use stats to relate your differential equation model to real data in your mathematical biology field? (Likely not answerable here, but maybe a link.)
Well, it might be a little old but still applicable I think –
‘The population went up and down, and so did the model’’ is not totally unjustified as a caricature of the way in which ecological [and mathematical biology] models are often compared to data.’
[Wood, 2001; see http://www.esajournals.org/doi/abs/10.1890/0012-9615%282001%29071%5B0001:PSEM%5D2.0.CO;2 ]
A nice paper presenting one method for relating differential equations to data, including a classical mathematical biology/physiology example (Fitzhugh-Nagumo/Hodgkin-Huxley model) and with lots of discussion at the end from a roundtable of statisticians and others, is
[Ramsay et al. 2007; see http://onlinelibrary.wiley.com/doi/10.1111/j.1467-9868.2007.00610.x/full ]
A general perspective on mathematical biology that might be interesting is
http://wcmb-oxford.blogspot.co.uk/2013/12/perspective-on-mathematical-biology.html
To reemphasise it’s not that it can’t be done, even with relatively straightforward methods in principle, it’s the difference in emphasis/attention that is striking I think. In the first year or two of undergrad maths/physics/engineering one seems to start dealing with models that are already difficult to tackle in practice with what is taught in the first year or three of many standard undergrad stats courses.
An example – the simplest/dumbest approach to do parameter estimation for an ODE that doesn’t have an analytical solution would be to just use what amounts to nonlinear regression. Assuming you have observations for all state variables and your ODE solver outputs a solution ys(t;theta) for a given parameter set theta, you can just take yobs(t)= Normal(ys(t; theta), sigma^2) and away you go with least squares. This quickly throws up all sorts of difficulties though – local minima, the numerical cost of computing a solution for every parameter set, dealing with unobserved state variables, how to deal with model mis-specification, violations of assumptions on errors etc etc. I don’t remember a stats course that covered these problems in depth in this context despite the ubiquity of these models in science/engineering/math (could be my bad memory/lack of exposure).
Omaclaren: Thanks so much for these extremely interesting links! I hope others will comment on these methods and issues.
@omaclaren
I can sympathize as someone who came into stats from a non-statistical modeling background. You do touch on one of the appealing things about bayes as a non-statistician. I think there’s a bit more to it than being “something different” –
1. the inferred model is inherently a generative model that can be simulated. If one is interested in falsification, this has the advantage of an end result which is falsifiable by further information (by gelman’s pseudo-frequentist-ish “model checking” if you’d like). By contrast, when I assume hypothesis is correct because p < .05 (something that I think mayo is good about criticizing), i haven't been forced to explicitly state a well-defined and testable model.
2. the bayesian definition of probability maps directly into how modelers tend to think about underdetermination intuitively. The adhoc heuristic approach of "solutions within the plausible parameter space consistent with the data", when taken to its mathematical conclusion, is bayes theorem.
Something else which I think is between the lines here is that in mechanistic modeling, the state space is much more constrained and coupled by mechanistic relationships. It is possible to often still get things wrong (particularly when many possible mechanisms can map to the same trend), but the effective fewer degrees of freedom is how it's _sometimes_ possible for mechanistic modelers to make progress with a limited amount of data.
vl: Just on your point #1, because it is confused, and things are the opposite. You can’t falsify with a Bayesian computation. You get a posterior, thats it. You’d need to add a rule–for example one that take low posterior for H into falsifying H. That’s a disaster! Also disastrous are rules to “falsify H” because an outcome is unlikely under H, or because it is comparatively less likely under H than some other “catchall or point alternative” (the analysis differs greatly depending on which of many you choose). Besides, one of the big advantages of Bayes is supposed to be to get a posterior probability on hypotheses rather than falsifying (or at least a comparative ratio). We error statisticians falsify, or provide evidence of discrepancies–and our inferences are properly qualified by error probabilities (wheres things like likelihood ratios mean different things from case to case). The reason Gelman is prepared to erect falsification rules is simply that he rejects the idea of inductive inference by assigning posteriors or Bayes factors.
No time to note further confusions, please search for table of contents of this blog to read relevant posts and/or my publications, linked to on this page.
No confusion about that point. I’m fine with stepping outside the model or outside bayesian inference entirely to evaluate it – hence “by gelman’s pseudo-frequentist-ish “model checking” if you’d like.”
Alternatively, Kruschke would probably prefer that I should make an even larger model which encompasses my space of models to do the model checking.
Personally I don’t feel that strongly about this either way. I’m more interested in getting a correct answer than strictly following one procedure or another religiously.
One reason I can live with some degree of incoherence when it comes to model selection (or falsification) is because there’s always this paradox – it’s impossible to fully enumerate the space of explanations (models) with 100% certainty, without enumerating the space of explanations it’s impossible to evaluate the probability that a selected model is correct. I don’t think there’s any way around that.
Changing the aim to something other than finding the plausibility of the model being correct (which seems to be one of the tenets of the severity approach) doesn’t do me much good as a practitioner if I still end up with the incorrect inference with high frequency.
I don’t see this as a pro- or anti- bayes view, it’s simply an acknowledgement that there’s no way to escape that no model selection procedure is immune to errors in the assumptions which underlie the procedure.
Of course, the ideal is to focus on the study design and restrict the space of explanations to such a degree that it’s easy for any procedure to deduce the “truth”, where the inverse problem is trivial (and perhaps doesn’t require statistics at all).
Nevertheless, I’m still interested in statistical methods because in practice there are always problems and experiments that lie somewhere in between of unambiguous causal identification and complete underdetermination. Even if statistics and inference doesn’t get you a solution in these cases, at least it can give you a sense of where you are on the spectrum.
(it’s probably time to get off the blogosphere and actually do something with my vacation time…)
I was going to make the same point but Mayo already did. I have a hard time seeing Bayesian models as useful for confirmation or testing, as they produce a posterior prob or post distr as a result. Given the underlying philosophy, I cannot see that as helping draw conclusions. No error probabilities. Prediction and exploratory work may be different.
@byrd that’s a bit of a circular argument. I doubt we’re going to have agreement, but here’s one more angle.
I’m fine with using sampling distributions and error probabilities when they are matched to a corresponding well-defined randomization process. However, this probably describes a small fraction of the data that statisticians are analyzing these days in science and elsewhere.
In all other scenarios, one is almost always facing varying degrees of underdetermination or partial identification. There’s an interplay between these problems and the “mechanistic” modeling being discussed above as well as other forms of borrowing information because these are one way of introducing bias to achieve identifiability and not fitting noise in the bias-variance sense. In these settings, analyzing data with respect to imagined randomization processes is far more fanciful than constructing a prior distribution.
You can dismiss all these scenarios as “exploratory” if you’d like but please don’t lump me in with the AI training/prediction crowd just because loss functions matter to me (as well as to anyone else that’s held responsible for their inferences being correct).
vl: You don’t need that data were generated by literally by a well defined random process for error probabilities to be relevant to inference. They are hypothetical and one can simulate the error probabilities as well as the sampling distribution (whether on a computer or on paper). These are what matter for severity assessments in inference (in non behavioristic settings).
Nor does caring about error assessment and control mean you want a loss function.
Likely causing to understand is so much harder than causing to believe things that are comforting or in one’s self interest to believe.
Another issue, is when statisticians choose to work with life scientists they need to decide between making them happy versus enabling them to do be better science. The latter can be painful and also risky if the life scientist is paying. People like to think they can do things and often are not as critical as they should be when someone with more expertise advises them they can. Sometimes will they search for can do statistician without realising that means the statistician is naïve about the difficulties.
I know this happens, I don’t know how often, but even if it’s a minority it keeps the nonsense going. An example would be a statistician at an Ivey league medical school who confided that they stopped talking about multiplicity problems when they noticed scientists would gravitate to working with other statisticians that did not ask about that.
Keith: Well Jim Berger and others seem to think the Bayesians have the magic when it comes to dealing with multiplicity, and can avoid those cumbersome adjustments (p. 30).
Click to access Purdue_Symposium_2012_Jim_Berger_Slides.pdf
More puzzling are the ways Bayes factors (e.g., pp. 19-20) are sold as the correct frequentist (conditional) error probabilities…This connects to a Berger paper I once commented on, and of course to my last post.
What is the fundamental distinction between frequencies in screening vs. hypotheses? Aren’t they both ultimately appraisals of hidden states of nature?
Bayesians don’t believe they can magically avoid doing cumbersome adjustments. The adjustment is folded into the base rate/shrinkage/prior model rather than a multiple comparison adjustment. Matt Stephens has written about the analogy and cases when they’re equivalent in one of his reviews.
One issue I have with multiple comparison adjustments is that their effects on frequencies of errors are inconsistent as power changes, but this requires the kind of “frequency of correctness” analysis that you’re not a fan of.
vl: Who is Matt Stevens? Can you send a link?
He’s a statistician who does work in genomics. I’d wouldn’t include him on the personalized medicine hype crowd. He does work in bayesian methods and advocates them, but his approach seems to be more practical than polemical.
Here’s the review:
http://www.nature.com/nrg/journal/v10/n10/abs/nrg2615.html
The relevant passage is box 1. Pretty simple stuff and it doesn’t cover the shrinkage aspect of the bayesian approach to multiple comparisons (kruschke and gelman cover that elsewhere), but that’s fine. The audience here is for applied researchers in the genetics/genomics, most of whom are not very adept or familiar with bayesian statistics.
Mayo:
Jim did state “Bayesian analysis deals with multiplicity testing solely through the assignment of prior probabilities to models or hypotheses.” and that is a mathematical fact and to re quote Churchill “You cannot ask us to take sides against arithmetic.” But one can still get the data model wrong and or have difficulty properly interpreting posterior quantities (e.g. a Bayes Factor of 8 is stronger than 4 but is it twice as strong or strong enough to reject H0?)
Jim is taking a position on matters that are not yet widely settled where as in Stephen’s post his material does not seem at all controversial. Yes there are likely many statisticians who are unaware of these issues but most would understand them if they read Stephen’s papers and very few would disagree.
So he has been writing about this since 2001 with seemingly little impact. Perhaps there is an avoidance by other statisticians (in pharma and regulatory agencies) of being a negative nelly matched with an attraction to all the exciting highly complex statistical work that would be entailed in the glossy view of personalised medicine everywhere.
Keith: I think I’m not clear on your saying “So he has been writing about this since 2001 with seemingly little impact.” I take it “he” is Senn now? At first I thought you meant Berger.
(Just to be clear: What is it that Senn is seemingly having little impact on (I mean in this particular post)? The tendency to suppose they know the response rates from this type of data? Sorry if I’m mistaking your referent.)
“You cannot ask us to take sides against arithmetic.” But I can ask them to take sides against a particular use of arithmetic in inference, if it fails to adequately take account of some features we would like inferences to take account of.
Anyway, I was responding to Steven McKinney.
Mayo:
Yup, referring Senn and that his work seems to have done little to reduce the excitement about personalised medicine when the formidable obstacles (poor economy of research) should be clear to most statisticians.
> But I can ask them to take sides against a particular use of arithmetic
I agree with that but your comment “Bayesians have the magic” suggested something else to me.
And you did address the comment to me “Keith: Well Jim Berger” …
Keith: Yes,I was replying to you on “they stopped talking about multiplicity problems when they noticed scientists” worked with those who ignored that, but in relation to what McKinney wrote rather than directly in relation to what Senn wrote. Sorry for any confusion, I WAS talking to you (to give an example from J. Berger).
I plead guilty to lack of impact. People just love the idea of personalised medicine. The reality is very different, with one dose fits all (no distinction between men & women and, often, children) being very common.
Keith is right that multiplicity is dealt with in the Bayesian approach through prior distributions. This avoids (in theory!) a difficulty with the frequentist approach, which requires an agreed (but in practice arbitrary) denominator for adjustment. In drug development the rates to control are usually taken to be ‘per trial’ rather than (say) the more stringent ‘per development programme’ or the less stringent ‘per test’. There is, however, no compelling logical reason for this.
@stephensenn for what it’s worth, I’m positioned to have some impact on these issues and I personally follow your writings with much interest.
I the difficulty is a case of wishful thinking + it’s hard to be the bearer of bad news.
I do think there is a spectrum though, as the personalization can come from varying degrees of mechanistic rationales. I would submit as a success the case of HIV (cancer also seems to be following a similar route). Beyond these cases where there’s a mechanistic line from drug resistance to treatment choice though, the analysis being done in genomics can be pretty bad.
Speaking of multiple comparisons, the naivete about multiple comparisons in this field is startling. People think they’re supposed to do it, but would have no comprehension of the interpretational issues you just described.
Pingback: S. Senn: “Painful dichotomies” (Guest Post) | Error Statistics Philosophy